Category: number theory

Some weeks ago, Robert Kucharczyk and Peter Scholze found a topological realisation of the ‘hopeless’ part of the absolute Galois group $\mathbf{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$. That is, they constructed a compact connected space $M_{cyc}$ such that etale covers of it correspond to Galois extensions of the cyclotomic field $\mathbb{Q}_{cyc}$. This gives, at least in theory, a handle on the hopeless part of the Galois group $\mathbf{Gal}(\overline{\mathbb{Q}}/\mathbb{Q}_{cyc})$, see the previous post in this series.

Here, we will get halfway into constructing $M_{cyc}$. We will try to understand the topology of the prime ideal spectrum $\mathbf{Spec}(\mathbb{C}[\overline{\mathbb{Q}}^{\times}])$ of the complex group algebra of the multiplicative group $\overline{\mathbb{Q}}^{\times}$ of all non-zero algebraic numbers.

[section_title text=”Pontryagin duals”]

Take an Abelian locally compact group $A$ (for example, an Abelian group equipped with the discrete topology), then its Pontryagin dual $A^{\vee}$ is the space of all continuous group morphisms $A \rightarrow \mathbb{S}^1$ to the unit circle $\mathbb{S}^1$ endowed with the compact open topology.

There are these topological properties of the locally compact group $A^{\vee}$:

– $A^{\vee}$ is compact if and only if $A$ has the discrete topology,

– $A^{\vee}$ is connected if and only if $A$ is a torsion free group,

– $A^{\vee}$ is totally disconnected if and only if $A$ is a torsion group.

If we take the additive group of rational numbers with the discrete topology, the dual space $\mathbb{Q}^{\vee}$ is the one-dimensional solenoid

It is a compact and connected group, but is not path connected. In fact, it path connected components can be identified with the finite adele classes $\mathbb{A}_f/\mathbb{Q} = \widehat{\mathbb{Z}}/\mathbb{Z}$ where $\widehat{\mathbb{Z}}$ is the ring of profinite integers.

Keith Conrad has an excellent readable paper on this fascinating object: The character group of $\mathbb{Q}$. Or you might have a look at this post.

[section_title text=”The multiplicative group of algebraic numbers”]

A torsion element $x$ in the multiplicative group $\overline{\mathbb{Q}}^{\times}$ of all algebraic numbers must satisfy $x^N=1$ for some $N$ so is a root of unity, so we have the exact sequence of Abelian groups

$0 \rightarrow \pmb{\mu}_{\infty} \rightarrow \overline{\mathbb{Q}}^{\times} \rightarrow \overline{\mathbb{Q}}^{\times}_{tf} \rightarrow 0$

where the last term is the maximal torsion-free quotient of $\overline{\mathbb{Q}}^{\times}$. By Pontryagin duality this gives us an exact sequence of compact topological groups

$0 \rightarrow (\overline{\mathbb{Q}}^{\times}_{tf})^{\vee} \rightarrow (\overline{\mathbb{Q}}^{\times})^{\vee} \rightarrow \pmb{\mu}^{\vee}_{\infty} \rightarrow 0$

Here, the left-most space is connected and $\pmb{\mu}^{\vee}_{\infty}$ is totally disconnected. That is, the connected components of $(\overline{\mathbb{Q}}^{\times})^{\vee}$ are precisely the translates of the connected subgroup $(\overline{\mathbb{Q}}^{\times}_{tf})^{\vee}$.

[section_title text=”Prime ideal spectra”]

The short exact sequence of Abelian groups gives a short exact sequence of the corresponding group schemes

$0 \rightarrow \mathbf{Spec}(\mathbb{C}[\overline{\mathbb{Q}}^{\times}_{tf}]) \rightarrow \mathbf{Spec}(\mathbb{C}[\overline{\mathbb{Q}}^{\times}] \rightarrow \mathbf{Spec}(\mathbb{C}[\pmb{\mu}_{\infty}]) \rightarrow 0$

The torsion free abelian group $\overline{\mathbb{Q}}^{\times}_{tf}$ is the direct limit $\underset{\rightarrow}{lim}~M_i$ of finitely generated abelian groups $M_i$ and as the corresponding group algebra $\mathbb{C}[M_i] = \mathbb{C}[x_1,x_1^{-1},\cdots, x_k,x_k^{-1}]$, we have that $\mathbf{Spec}(\mathbb{C}[M_i])$ is connected. But then this also holds for

$\mathbf{Spec}(\mathbb{C}[\overline{\mathbb{Q}}^{\times}_{tf}]) = \underset{\leftarrow}{lim}~\mathbf{Spec}(\mathbb{C}[M_i])$

The underlying group of $\mathbb{C}$-points of $\mathbf{Spec}(\mathbb{C}[\pmb{\mu}_{\infty}])$ is $\pmb{\mu}_{\infty}^{\vee}$ and is therefore totally disconnected. But then we have

$\pi_0(\mathbf{Spec}(\mathbb{C}[\overline{\mathbb{Q}}^{\times}]) \simeq \pi_0(\mathbf{Spec}(\mathbb{C}[\pmb{\mu}_{\infty}]) \simeq \pmb{\mu}_{\infty}^{\vee}$

and, more importantly, for the etale fundamental group

$\pi_1^{et}(\mathbf{Spec}(\mathbb{C}[\overline{\mathbb{Q}}^{\times}],x) \simeq \pi_1^{et}(\mathbf{Spec}(\mathbb{C}[\overline{\mathbb{Q}}^{\times}_{tf}],y)$

So, we have to compute the latter one. Again, write the torsion-free quotient as a direct limit of finitely generated torsion-free Abelian groups and recall that connected etale covers of $\mathbf{Spec}(\mathbb{C}[M_i])=\mathbf{Spec}(\mathbb{C}[x_1,x_1^{-1},\cdots,x_k,x_k^{-1}])$ are all of the form $\mathbf{Spec}(\mathbb{C}[N])$, where $N$ is a subgroup of $M_i \otimes \mathbb{Q}$ that contains $M_i$ with finite index (that is, adjoining roots of the $x_i$).

Again, this goes through the limit and so a connected etale cover of $\mathbf{Spec}(\mathbb{C}[\overline{\mathbb{Q}}^{\times}_{tf}])$ would be determined by a subgroup of the $\mathbb{Q}$-vectorspace $\overline{\mathbb{Q}}^{\times}_{tf} \otimes \mathbb{Q}$ containing $\overline{\mathbb{Q}}^{\times}_{tf}$ with finite index.

But, $\overline{\mathbb{Q}}^{\times}_{tf}$ is already a $\mathbb{Q}$-vectorspace as we can take arbitrary roots in it (remember we’re using the multiplicative structure). That is, $\mathbf{Spec}(\mathbb{C}[\overline{\mathbb{Q}}^{\times}])$ is simply connected!

[section_title text=”Bringing in the Galois group”]

Now, we’re closing in on the mysterious space $M_{cyc}$. Clearly, it cannot be the complex points of $\mathbf{Spec}(\mathbb{C}[\overline{\mathbb{Q}}^{\times}])$ as this has no proper etale covers, but we still have to bring the Galois group $\mathbf{Gal}(\overline{\mathbb{Q}}/\mathbb{Q}_{cyc})$ into the game.

The group algebra $\mathbb{C}[\overline{\mathbb{Q}}^{\times}]$ is a commutative and cocommutative Hopf algebra, and all the elements of the Galois group act on it as Hopf-automorphisms, so it is natural to consider the fixed Hopf algebra

$H_{cyc}=\mathbb{C}[\overline{\mathbb{Q}}^{\times}]^{\mathbf{Gal}(\overline{\mathbb{Q}}/\mathbb{Q}_{cyc})}$

This Hopf algebra has an interesting alternative description as a subalgebra of the Witt ring $W(\mathbb{Q}_{cyc})$, bringing it into the realm of $\mathbb{F}_1$-geometry.

This ring of Witt vectors has as its underlying set of elements $1 + \mathbb{Q}_{cyc}[[t]]$ of formal power series in $\mathbb{Q}_{cyc}[[t]]$. Addition on this set is defined by multiplication of power series. The surprising fact is that we can then put a ring structure on it by demanding that the product $\odot$ should obey the rule that for all $a,b \in \mathbb{Q}_{cyc}$ we have

$(1-at) \odot (1-bt) = 1 – ab t$

In this mind-boggling ring the Hopf algebra $H_{cyc}$ is the subring consisting of all power series having a rational expression of the form

$\frac{1+a_1t+a_2t^2+ \cdots + a_n t^n}{1+b_1 t + b_2 t^2 + \cdots + b_m t^m}$

with all $a_i,b_j \in \mathbb{Q}_{cyc}$.

We can embed $\pmb{\mu}_{\infty}$ by sending a root of unity $\zeta$ to $1 – \zeta t$, and then the desired space $M_{cyc}$ will be close to

$\mathbf{Spec}(H_{cyc} \otimes_{\mathbb{Z}[\pmb{\mu}_{\infty}]} \mathbb{C})$

but I’ll spare the details for another time.

In case you want to know more about the title-picture, quoting from John Baez’ post The Beauty of Roots:

“Sam Derbyshire decided to to make a high resolution plot of some roots of polynomials. After some experimentation, he decided that his favorite were polynomials whose coefficients were all 1 or -1 (not 0). He made a high-resolution plot by computing all the roots of all polynomials of this sort having degree ≤ 24. That’s $2^{24}$ polynomials, and about $24 \times 2^{24}$ roots — or about 400 million roots! It took Mathematica 4 days to generate the coordinates of the roots, producing about 5 gigabytes of data.”

Comments closed

We know embarrassingly little about the symmetries of the roots of all polynomials with rational coefficients, or if you prefer, the absolute Galois group $Gal(\overline{\mathbb{Q}}/\mathbb{Q})$.

In the title picture the roots of polynomials of degree $\leq 4$ with small coefficients are plotted and coloured by degree: blue=4, cyan=3, red=2, green=1. Sums and products of roots are again roots and by a symmetry we mean a map on all roots, sending sums to sums and products to products and leaving all the green dots (the rational numbers) fixed.

John Baez has an excellent post on the beauty of roots, including a picture of all polynomials of degree $\leq 5$ with integer coefficients between $-4$ and $4$ and, this time, colour-coded by: grey=2, cyan=3, red=4 and black=5.

In both pictures there’s a hint of the unit circle, black in the title picture and spanning the ‘white gaps’ in the picture above.

If we’d only consider the sub-picture of all (sums and products of) roots including the rational numbers on the horizontal axis and the roots of unity on the unit circle we’d get the cyclotomic field $\mathbb{Q}_{cyc} = \mathbb{Q}(\mu_{\infty})$. Here we know all symmetries: they are generated by taking powers of the roots of unity. That is, we know all about the Galois group $Gal(\mathbb{Q}_{cyc}/\mathbb{Q})$.

The ‘missing’ symmetries, that is the Galois group $Gal(\overline{\mathbb{Q}}/\mathbb{Q}_{cyc})$ remained a deep mystery, until last week…

[section_title text=”The oracle speaks”]

On september 15th, Robert Kucharczyk and Peter Scholze (aka the “oracle of arithmetic” according to Quanta-magazine) arXived their paper Topological realisations of absolute Galois groups.

They discovered a concrete compact connected Hausdorff space $M_{cyc}$ such that Galois extensions of $\mathbb{Q}_{cyc}$ correspond to connected etale covers of $M_{cyc}$.

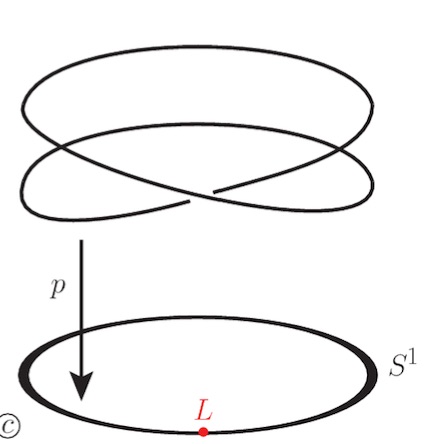Let’s look at a finite field $\mathbb{F}_p$. Here, Galois extensions of $\mathbb{F}_p$ (and there is just one such extension of degree $n$, upto isomorphism) correspond to connected etale covers of the circle $S^1$.

An etale map $X \rightarrow S^1$ is such that every circle point has exactly $n$ pre-images. Here again, up to homeomorphism, there is a unique such $n$-fold cover of $S^1$ (the picture on the left gives the cover for $n=2$).

.

If we replace $\mathbb{F}_p$ by the cyclotomic field $\mathbb{Q}_{cyc}$ then the compact space $M_{cyc}$ replaces the circle $S^1$. So, if we take a splitting polynomial of degree $n$ with coefficients in $\mathbb{Q}_{cyc}$, then there is a corresponding etale $n$-fold cover $X \rightarrow M_{cyc}$ such that for a specific point $p$ in $M_{cyc}$ its pre-images correspond to the roots of the polynomial. Nice!

Sadly, there’s a catch. Even though we have a concrete description of $M_{cyc}$ it turns out to be a horrible infinite dimensional space, it is connected but not path-connected, and so on.

Even Peter Scholze says it’s unclear whether new results can be proved from this result (see around 39.15 in his Next Generation Outreach Lecture).

Btw. if your German is ok, this talk is a rather good introduction to classical Galois theory and etale fundamental groups, including the primes=knots analogy.

[section_title text=”the imaginary field with one element”]

Of course there’s no mention of it in the Kucharczyk-Scholze paper, but this result is excellent news for those trying to develop a geometry over the imaginary field with one element $\mathbb{F}_1$ and hope to apply this theory to problems in number theory.

As a side remark, some of these people have just published a book with the EMS Publishing House: Absolute arithmetic and $\mathbb{F}_1$-geometry

The basic idea is that the collection of all prime numbers, $\mathbf{Spec}(\mathbb{Z})$ is far too large an object to be a terminal object (as it is in schemes). One should therefore extend the setting of schemes to so called $\mathbb{F}_1$-schemes, in which $\mathbf{Spec}(\mathbb{Z})$ is some higher dimensional object.

Initially, one hoped that $\mathbf{Spec}(\mathbb{Z})/\mathbb{F}_1$ might look like a curve, so that one could try to mimick Weil’s proof of the Riemann hypothesis for curves to prove the genuine Riemann hypothesis.

But, over the last decade it became clear that $\mathbf{Spec}(\mathbb{Z})/\mathbb{F}_1$ looks like an infinite dimensional space, a bit like the space $M_{cyc}$ above.

I’ll spare this to a couple of follow-up posts, but for now I’ll leave you with the punchline:

The compact connected Hausdorff space $M_{cyc}$ of Kucharczyk and Scholze is nothing but the space of complex points of $\mathbf{Spec}(\mathbb{Q}_{cyc})/\mathbb{F}_1$!

Comments closed