Conway’s Big Picture consists of all pairs of rational numbers $M,\frac{g}{h}$ with $M > 0$ and $0 \leq \frac{g}{h} < 1$ with $(g,h)=1$. Recall from last time that $M,\frac{g}{h}$ stands for the lattice
\[
\mathbb{Z} (M \vec{e}_1 + \frac{g}{h} \vec{e}_2) \oplus \mathbb{Z} \vec{e}_2 \subset \mathbb{Q}^2 \]
and we associate to it the rational $2 \times 2$ matrix
\[
\alpha_{M,\frac{g}{h}} = \begin{bmatrix} M & \frac{g}{h} \\ 0 & 1 \end{bmatrix} \]
If $M$ is a natural number we write $M \frac{g}{h}$ and call the corresponding lattice number-like, if $g=0$ we drop the zero and write $M$.
The Big Picture carries a wealth of structures. Today, we will see that it can be factored as the product of Bruhat-Tits buildings for $GL_2(\mathbb{Q}_p)$, over all prime numbers $p$.
Here’s the factor-building for $p=2$, which is a $3$-valent tree:
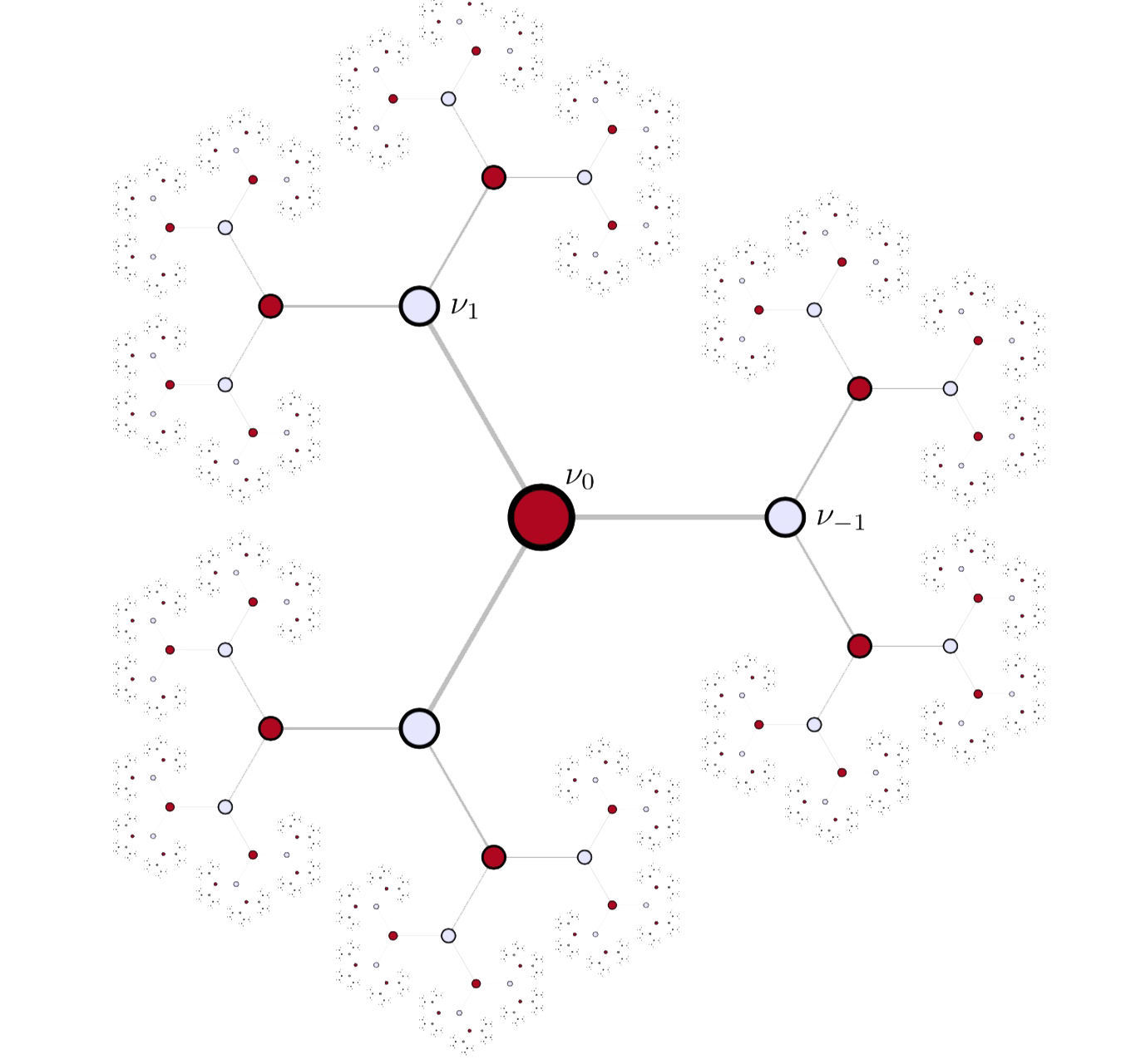
To see this, define the distance between lattices to be
\[
d(M,\frac{g}{h}~|~N,\frac{i}{j}) = log~Det(q(\alpha_{M,\frac{g}{h}}.\alpha_{N,\frac{i}{j}}^{-1})) \]
where $q$ is the smallest strictly positive rational number such that $q(\alpha_{M,\frac{g}{h}}.\alpha_{N,\frac{i}{j}}^{-1}) \in GL_2(\mathbb{Z})$.
We turn the Big Picture into a (coloured) graph by drawing an edge (of colour $p$, for $p$ a prime number) between any two lattices distanced by $log(p)$.
\[
\xymatrix{M,\frac{g}{h} \ar@[red]@{-}[rr]|p & & N,\frac{i}{j}} \qquad~\text{iff}~\qquad d(M,\frac{g}{h}~|~N,\frac{i}{j})=log(p) \]
The $p$-coloured subgraph is $p+1$-valent.
The $p$-neighbours of the lattice $1 = \mathbb{Z} \vec{e}_1 \oplus \mathbb{Z} \vec{e}_2$ are precisely these $p+1$ lattices:
\[
p \qquad \text{and} \qquad \frac{1}{p},\frac{k}{p} \qquad \text{for} \qquad 0 \leq k < p \]
And, multiplying the corresponding matrices with $\alpha_{M,\frac{g}{h}}$ tells us that the $p$-neighbours of $M,\frac{g}{h}$ are then these $p+1$ lattices:
\[
pM,\frac{pg}{h}~mod~1 \qquad \text{and} \qquad \frac{M}{p},\frac{1}{p}(\frac{g}{h}+k)~mod~1 \qquad \text{for} \qquad 0 \leq k < p \]
Here's part of the $2$-coloured neighbourhood of $1$
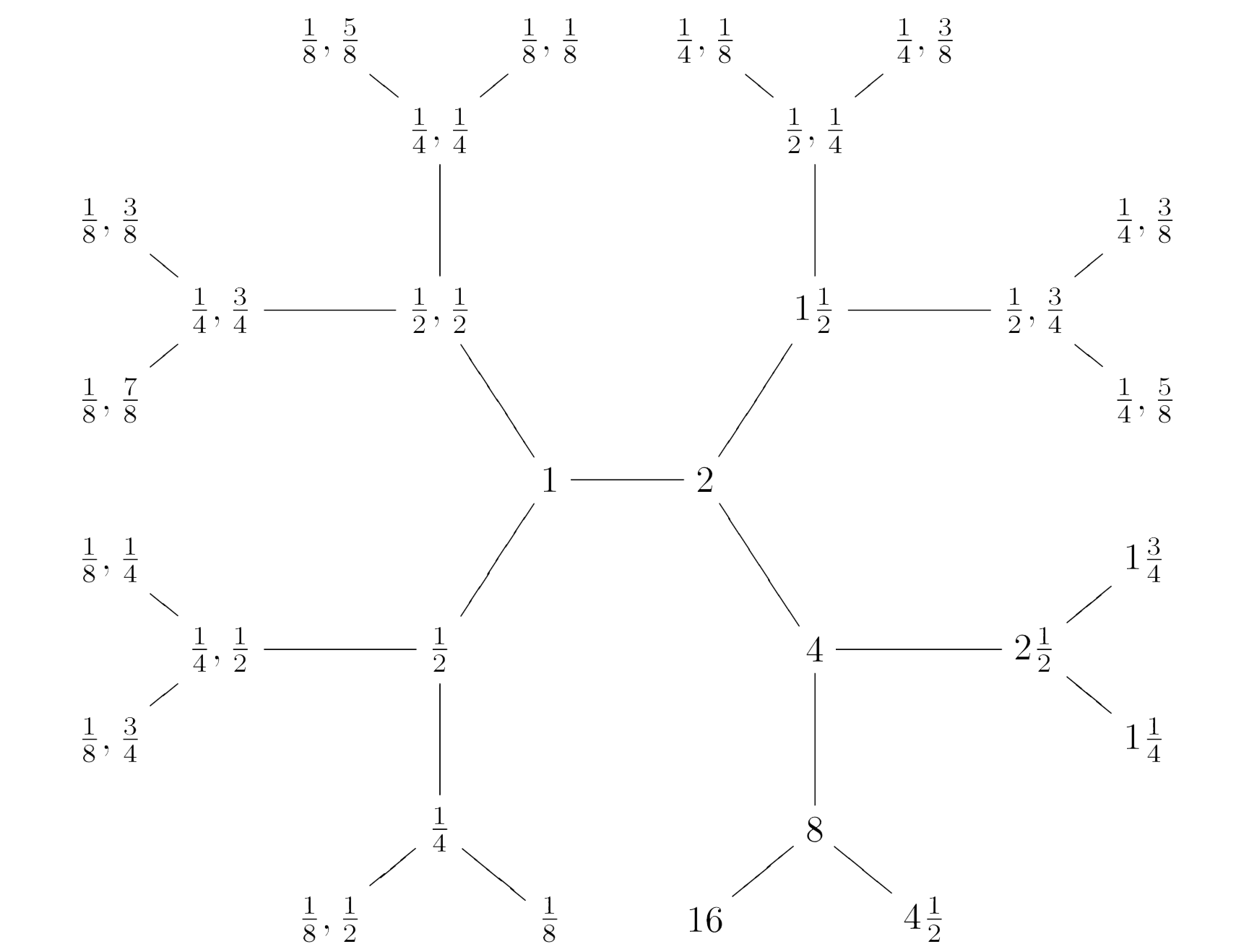
To check that the $p$-coloured subgraph is indeed the Bruhat-Tits building of $GL_2(\mathbb{Q}_p)$ it remains to see that it is a tree.
For this it is best to introduce $p+1$ operators on lattices
\[
p \ast \qquad \text{and} \qquad \frac{k}{p} \ast \qquad \text{for} \qquad 0 \leq k < p \]
defined by left-multiplying $\alpha_{M,\frac{g}{h}}$ by the matrices
\[
\begin{bmatrix} p & 0 \\ 0 & 1 \end{bmatrix} \qquad \text{and} \qquad \begin{bmatrix} \frac{1}{p} & \frac{k}{p} \\ 0 & 1 \end{bmatrix} \qquad \text{for} \qquad 0 \leq k < p \]
The lattice $p \ast M,\frac{g}{h}$ lies closer to $1$ than $M,\frac{g}{h}$ (unless $M,\frac{g}{h}=M$ is a number) whereas the lattices $\frac{k}{p} \ast M,\frac{g}{h}$ lie further, so it suffices to show that the $p$ operators
\[
\frac{0}{p} \ast,~\frac{1}{p} \ast,~\dots~,\frac{p-1}{p} \ast \]
form a free non-commutative monoid.
This follows from the fact that the operator
\[
(\frac{k_n}{p} \ast) \circ \dots \circ (\frac{k_2}{p} \ast) \circ (\frac{k_1}{p} \ast) \]
is given by left-multiplication with the matrix
\[
\begin{bmatrix} \frac{1}{p^n} & \frac{k_1}{p^n}+\frac{k_2}{p^{n-1}}+\dots+\frac{k_n}{p} \\ 0 & 1 \end{bmatrix} \]
which determines the order in which the $k_i$ occur.
A lattice at distance $n log(p)$ from $1$ can be uniquely written as
\[
(\frac{k_{n-l}}{p} \ast) \circ \dots \circ (\frac{k_{l+1}}{p} \ast) \circ (p^l \ast) 1 \]
which gives us the unique path to it from $1$.
The Big Picture itself is then the product of these Bruhat-Tits trees over all prime numbers $p$. Decomposing the distance from $M,\frac{g}{h}$ to $1$ as
\[
d(M,\frac{g}{h}~|~1) = n_1 log(p_1) + \dots + n_k log(p_k) \]
will then allow us to find minimal paths from $1$ to $M,\frac{g}{h}$.
But we should be careful in drawing $2$-dimensional cells (or higher dimensional ones) in this ‘product’ of trees as the operators
\[
\frac{k}{p} \ast \qquad \text{and} \qquad \frac{l}{q} \ast \]
for different primes $p$ and $q$ do not commute, in general. The composition
\[
(\frac{k}{p} \ast) \circ (\frac{l}{q} \ast) \qquad \text{with matrix} \qquad \begin{bmatrix} \frac{1}{pq} & \frac{kq+l}{pq} \\ 0 & 1 \end{bmatrix} \]
has as numerator in the upper-right corner $0 \leq kq + l < pq$ and this number can be uniquely(!) written as
\[
kq+l = up+v \qquad \text{with} \qquad 0 \leq u < q,~0 \leq v < p \]
That is, there are unique operators $\frac{u}{q} \ast$ and $\frac{v}{p} \ast$ such that
\[
(\frac{k}{p} \ast) \circ (\frac{l}{q} \ast) = (\frac{u}{q} \ast) \circ (\frac{v}{p} \ast) \]
which determine the $2$-cells
\[
\xymatrix{ \bullet \ar@[blue]@{-}[rr]^{\frac{u}{q} \ast} \ar@[red]@{-}[dd]_{\frac{v}{p} \ast} & & \bullet \ar@[red]@{-}[dd]^{\frac{k}{p} \ast} \\ & & \\ \bullet \ar@[blue]@{-}[rr]_{\frac{l}{q} \ast} & & \bullet} \]
These give us the commutation relations between the free monoids of operators corresponding to different primes.
For the primes $2$ and $3$, relevant in the description of the Moonshine Picture, the commutation relations are
\[
(\frac{0}{2} \ast) \circ (\frac{0}{3} \ast) = (\frac{0}{3} \ast) \circ (\frac{0}{2} \ast), \quad
(\frac{0}{2} \ast) \circ (\frac{1}{3} \ast) = (\frac{0}{3} \ast) \circ (\frac{1}{2} \ast),
\quad
(\frac{0}{2} \ast) \circ (\frac{2}{3} \ast) = (\frac{1}{3} \ast) \circ (\frac{0}{2} \ast) \]
\[
(\frac{1}{2} \ast) \circ (\frac{0}{3} \ast) = (\frac{1}{3} \ast) \circ (\frac{1}{2} \ast), \quad
(\frac{1}{2} \ast) \circ (\frac{1}{3} \ast) = (\frac{2}{3} \ast) \circ (\frac{0}{2} \ast),
\quad
(\frac{1}{2} \ast) \circ (\frac{2}{3} \ast) = (\frac{2}{3} \ast) \circ (\frac{1}{2} \ast) \]