Category: math

Here’s batch 2 of my old google+ posts on ‘Inter Universal Teichmuller theory’, or rather on the number theoretic examples of Frobenioids.

June 5th, 2013

Mochizuki’s categorical prime number sieve

And now for the interesting part of Frobenioids1: after replacing a bunch of arithmetic schemes and maps between them by a huge category, we will reconstruct this classical picture by purely categorical means.

Let’s start with the simplest case, that of the ‘baby arithmetic Frobenioid’ dismantling $\mathbf{Spec}(\mathbb{Z}) (that is, the collection of all prime numbers) and replacing it by the category having as its objects

all $(a)$ where $a$ is a strictly positive rational number

and morphisms labeled by triples $(n,r,z)$ where $n$ and $z$ are strictly positive integers and $r$ is a strictly positive rational number and connecting two objects

\[
(n,r,z) : (a) \rightarrow (b) \quad \text{ if and only if } \quad a^n.z=b.r \]

Composition of morphisms is well-defined and looks like $(m,s,v) \circ (n,r,u) = (m.n,r^m.s,u^m.v)$ as one quickly checks.

The challenge is to recover all prime numbers back from this ‘Frobenioid’. We would like to take an object $(a)$ and consider the maps $(1,1,p)$ from it for all prime numbers $p$, but cannot do this as categorically we have to drop all labels of objects and arrows. That is, we have to recognize the map $(1,1,p)$ among all maps starting from a given object.

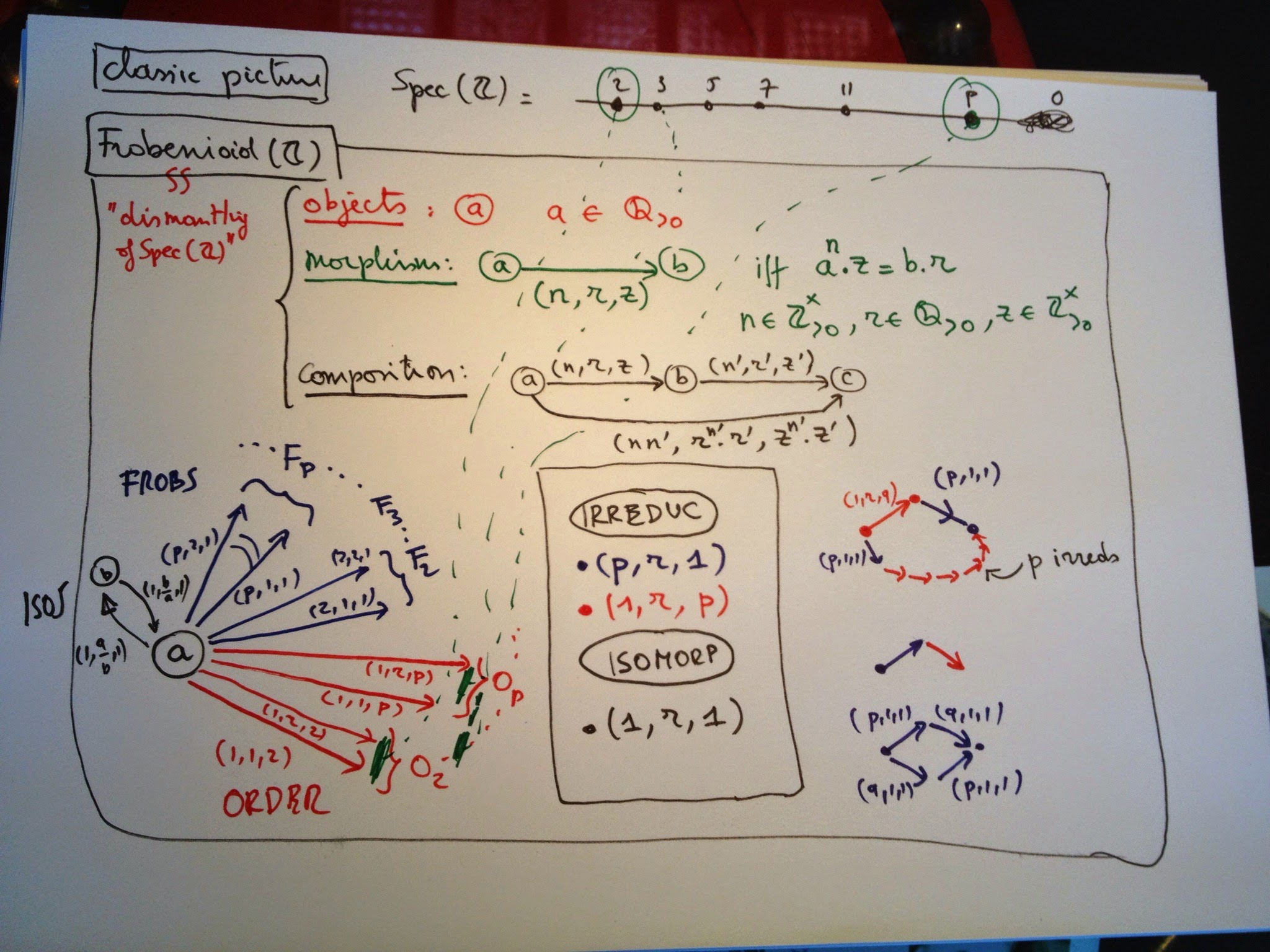
We can identify all isomorphisms in the category and check that they are precisely the morphisms labeled $(1,r,1)$. In particular, this implies that all objects are isomorphic and that there is a natural correspondence between arrows leaving $(a)$ and arrows leaving $(b)$ by composing them with the iso $(1,b/a,1) : (b) \rightarrow (a)$.

Another class of arrows we can spot categorically are the ‘irreducibles’, which are maps $f$ which are not isos but have the property that in any factorization $f=g \circ h$ either $g$ or $h$ must be an iso. One easily verifies from the composition rule that these come in two flavours:

– those of Frobenius type : $(p,r,1)$ for any prime number $p$
– those of Order type : $(1,r,p)$ for any prime number $p$

We would like to color the froBs Blue and the oRders Red, but there seems to be no way to differentiate between the two classes by purely categorical means, until you spot Mochizuki’s clever little trick.

start with a Red say $(1,r,q)$ for a prime number $q$ and compose it with the Blue $(p,1,1)$, then you get the morphism $(p,r^p,q^p)$ which you can factor as a composition of $p+1$ irreducibles

\[
(p,r^p,q^p) = (1,r,q) \circ (1,r,q) \circ …. \circ (1,r,q)o(p,1,1) \]

and if $p$ grows, so will the number of factors in this composition.

On the other hand, if you start with a Blue and compose it with either a Red or a Blue irreducible, the obtained map cannot be factored in more irreducibles.

Thus, we can identify the Order-type morphisms as those irreducibles $f$ for which there exists an irreducible $g$ such that the composition $g \circ f$ can be factored as the composition in at least $n$ irreducibles, where we can take n arbitrarily large.

Finally we say that two Reds out of $(a)$ are equivalent iff one is obtained from the other by composing with an isomorphism and it is clear that the equivalence classes are exactly the arrows labeled $(1,r,p)$ for fixed prime number $p$.

So we do indeed recover all prime numbers from the category.

Similarly, we can see that equivalence classes of Frobs from $(a)$ are of the form $(p,r,1)$ for fixed prime $p$. An amusing fact is that we can recover the prime $p$ for a Frob by purely categorical ways using the above long factorization of a composition with a Red.

There seems to be no categorical way to determine the prime number associated to an equivalence class of Order-morphisms though… Or, am i missing something trivial?

June 7th, 2013

Mochizuki’s Frobenioids for the Working Category Theorist

Many of you, including +David Roberts  +Charles Wells  +John Baez  (and possibly others, i didn’t look at all comments left on all reshares of the past 4 posts in this MinuteMochizuki project) hoped that there might be a more elegant category theoretic description of Frobenioids, the buzz-word apparently being ‘Grothendieck fibration’ …

Hence this attempt to deconstruct Frobenioids. Two caveats though:

– i am not a category theorist (the few who know me IRL are by now ROFL)
– these categories are meant to include all arithmetic information of number fields, which is a messy business, so one should only expect clear cut fibrations in easy situation such as principal ideal domains (think of the integers $\mathbb{Z}$).

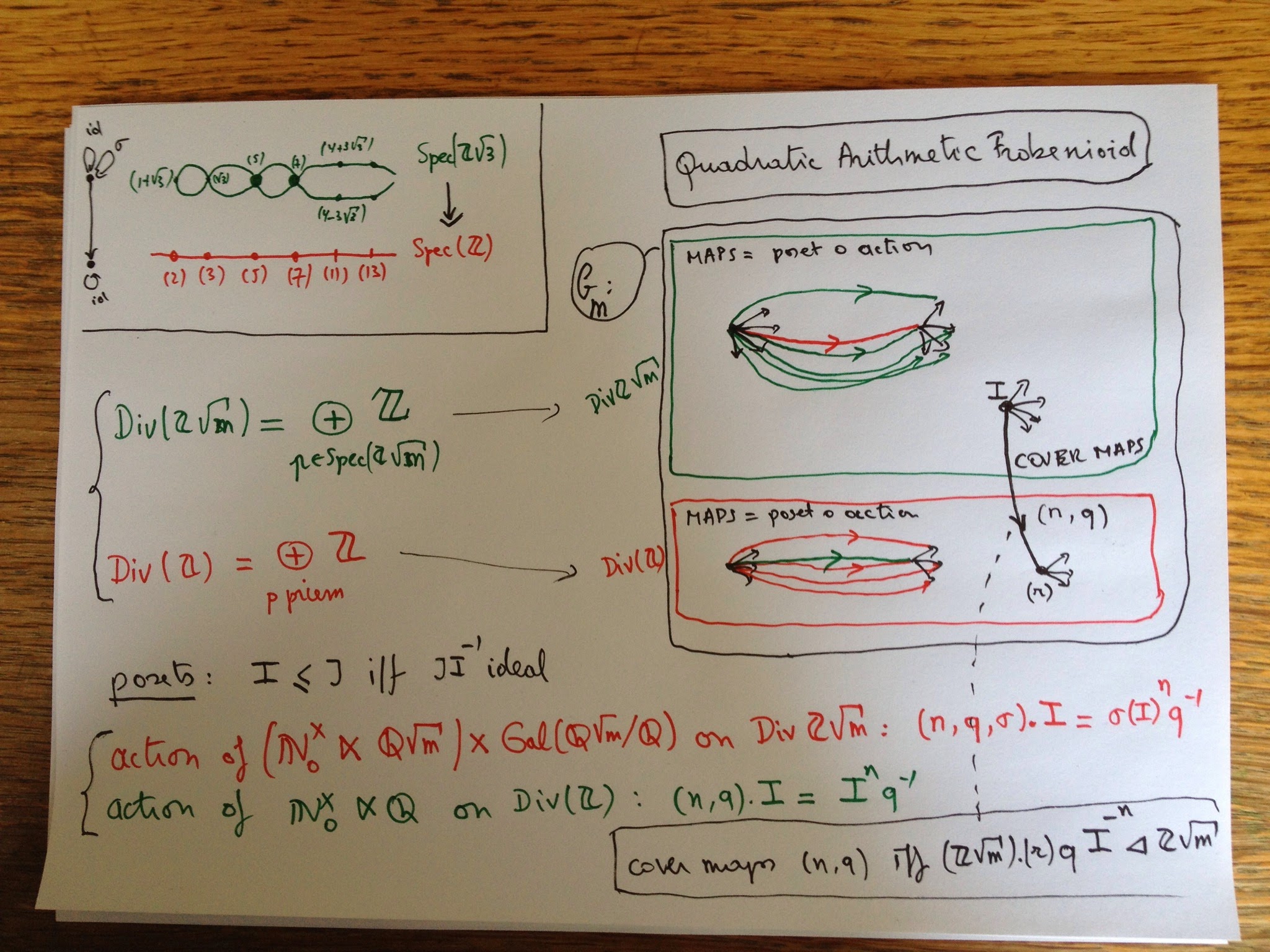
Okay, we will try to construct the Frobenioid associated to a number field $K$ (that is, a finite dimensional extension of the rationals $\mathbb{Q}$) with ring of integers $R$ (the integral closure of $\mathbb{Z}$ in $K$). For a concrete situation, look at the quadratic case.

The objects will be fractional ideals of K which are just the R-submodules $I$ of $K$ such that there in an $r$ in $R$ such that $I.r$ is a proper ideal of $R$. Dedekind showed that any such thing can be written uniquely as a product

\[
I = P_1^{a_1} … P_k^{a_k} \]

where the $P_i$ are prime ideals of $R$ and the $a_i$ are integers (if they are all natural numbers, I will be a proper ideal of $R$). Clearly, if one multiplies two fractional ideals $I$ and $J$, the result $I.J$ is again a fractional ideal, so they form a group and by Dedekind’s trick this group is the free Abelian group on all prime ideals of $R$.

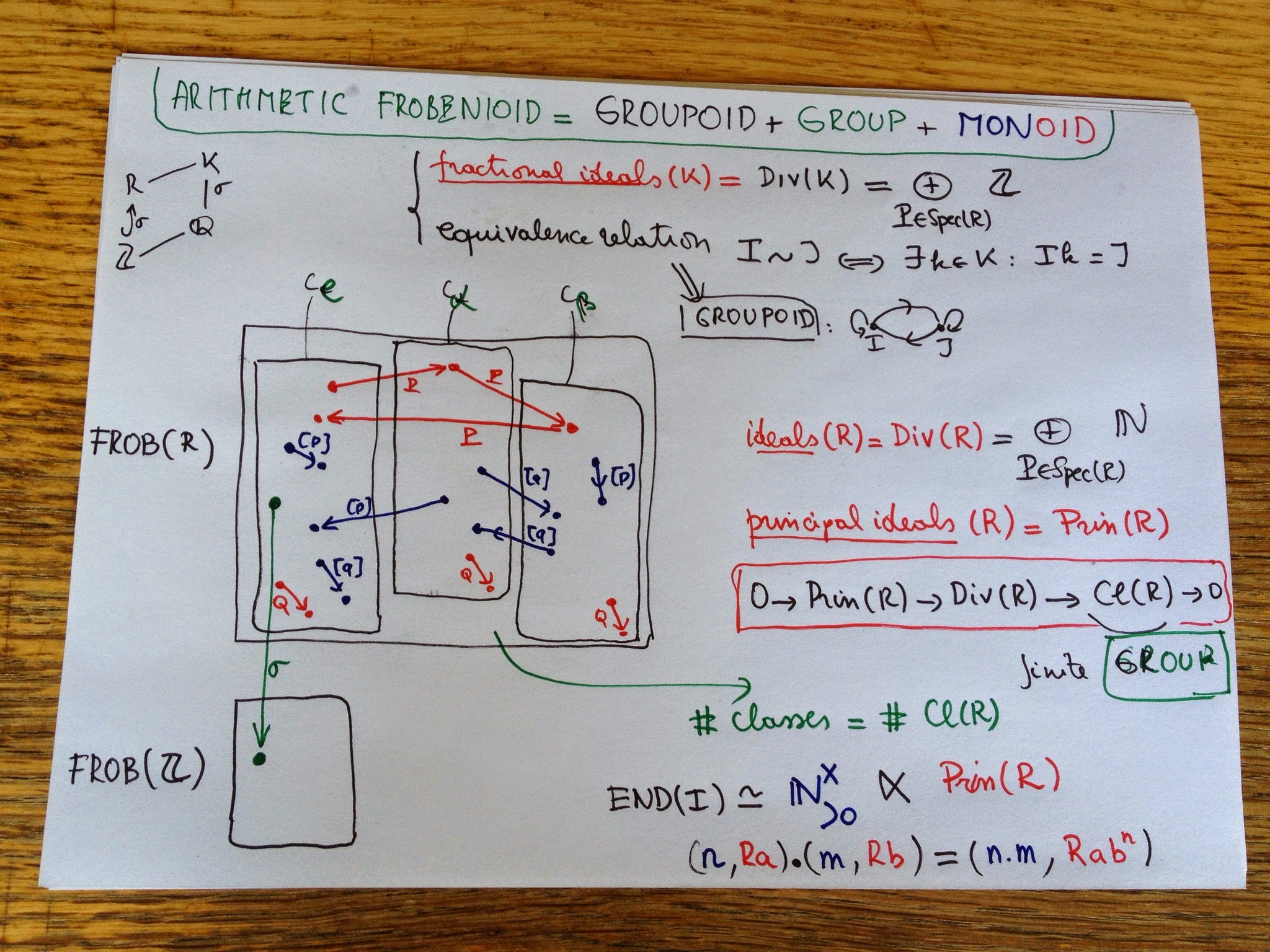
Next, we define an equivalence relation on this set, calling two fractional ideals $I$ and $J$ equivalent if there is a $k$ in $K$ such that $I=J.k$ (or if you prefer, if they are isomorphic as $R$-modules).

We have a set with an equivalence relation and hence a groupoid where these is a unique isomorphism between any two equivalent objects. This groupoid is precisely the groupoid of isomorphisms of the Frobenioid we’re after.

The number of equivalence classes is finite and these classes correspond to the element of a finite group $Cl(R)$ called the class group of $R$ which is the quotient group of ideals modulo principal ideals (so if your $R$ is a principal ideal domain there is just one component). The ‘groups’ corresponding to each connected component of the groupoid are all isomorphic to the quotient group of the units in $K$ by the units in $R$.

Next, we will add the other morphisms. By definition they are all compositions of irreducibles which come in 2 flavours:

– the order-morphisms $P$ for any prime ideal $P$ of $R$ sending $I$ to $I.P$. Typically, these maps switch between different equivalence classes (unless $P$ itself is principal). We can even explicitly compute small norm prime ideals which will generate all elements in the class group $Cl(R)$.
– the power-maps $[p]$ for any prime number $p$ which sends $I$ to $I^p$. The nature of these maps really depend on the order of the component in the finite group $Cl(R)$.

Well, that’s it basically for the layer of the Frobenioid corresponding to the number field $K$. (You have to repeat all this for any subfield between $\mathbb{Q}$ and $K$). A cute fact is that all endomorphism-monoids of objects in the layer of K are all isomorphic as abstract monoid to the skew-monoid

$\mathbb{N}^x_{>0} x Prin(R)$ of the multiplicative group of all strictly positive integers $n$ with the monoid of all principal ideals in R with multiplication defined by

\[
(n,Ra).(m,Rb)=(nm,Rab^n) \]

The only extra-type morphisms we still have to include are those between the different layers of the Frobenioid, the green ones which M calls the pull-back morphisms.
They are of the following form: if $R_1$ and $R_2$ are rings of integers in the fields $K_1$ contained in $K_2$, then for any ringmorphism $\sigma : R_1 \rightarrow R_2$ one can extend a fractional ideal $I$ of $R_1$ to $K_2$ by considering $R_2.\sigma(I)$. These then give the morphism $r_2\sigma(I) \rightarrow I$ and as we will see in a next instalment, they encode the splitting behaviour of prime ideals.

a question for category people

Take the simplest situation, that of the integers $\mathbb{Z}$. So, we have just a groupoid with extra morphisms generated by the order-maps $o_p$ and the power maps $f_p$. The endo-ring of any object is then isomorphic top the abstract group generated by the $f_p$ and $o_p$ and satisfying following relations

\[
o_p.o_q=o_q.o_p \]
\[
f_p.f_q=f_q.f_p \]
\[
f_p.o_q=o_q^p.f_p \]

My question now is: if for two different primes $p$ and $q$ i switch their role in the endo-ring of 1 object and propagate this via all isos to all morphisms, do i get a category equivalence? (or am i missing something?).  (tbc)

June 11th, 2013

my problem with Mochizuki’s Frobenioid1

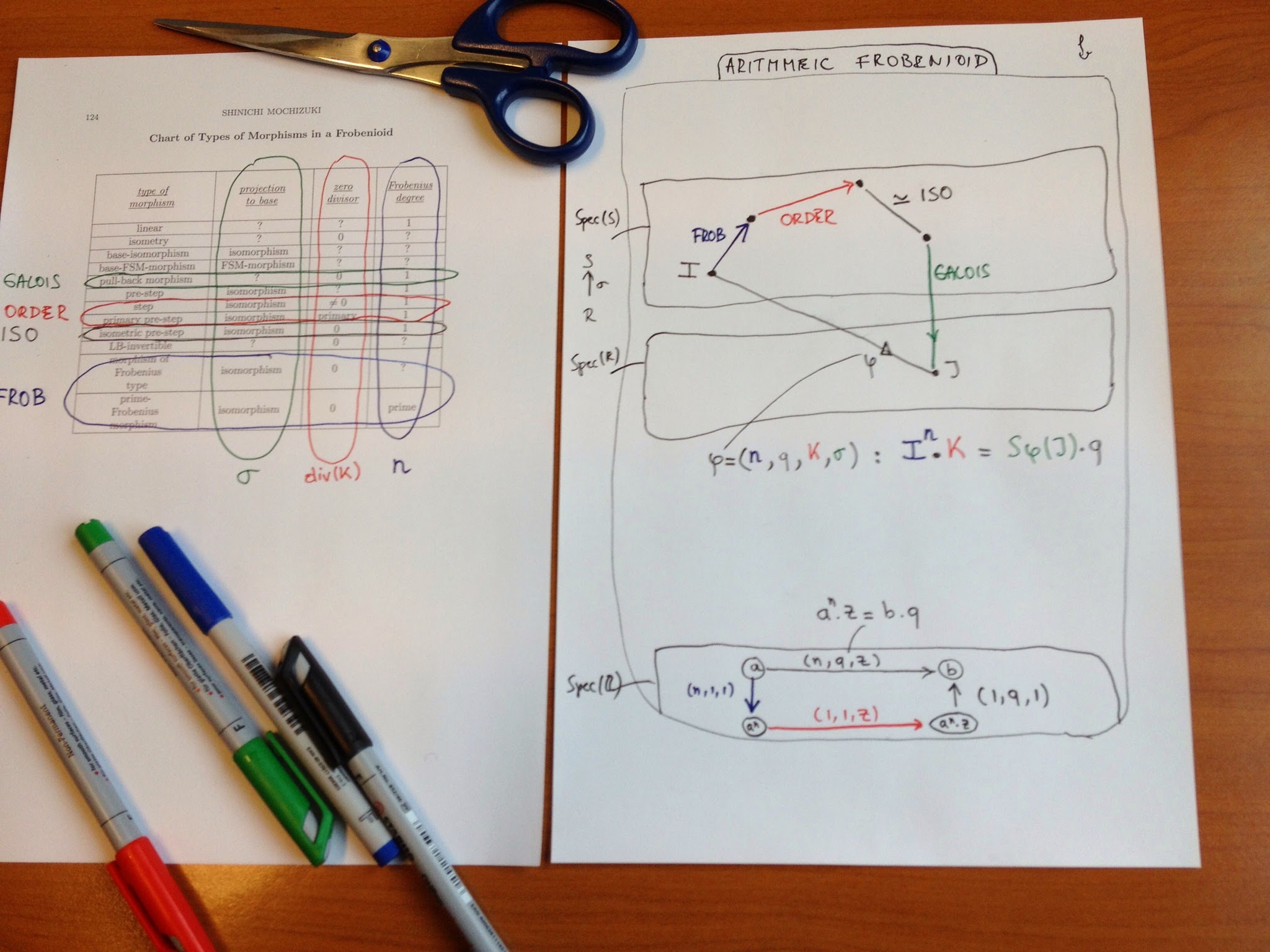
Let us see how much arithmetic information can be reconstructed from an arithmetic Frobenioids. Recall that for a fixed finite Galois extension $L$ of $\mathbb{Q}$ this is a category with objects all fractional ideals in subfields of $L$, and maps generated by multiplication-maps with ideals in rings of integers, power-maps and Galois-extension maps.

When all objects and morphisms are labeled it is quite easy to reconstruct the Galois field $L$ from it as well as all maps between prime spectra of rings of integers in intermediate fields, which after all was the intended use of Frobenioids, to ‘dismantle’ these arithmetic schemes and endow them with extra structure given by the power-maps.

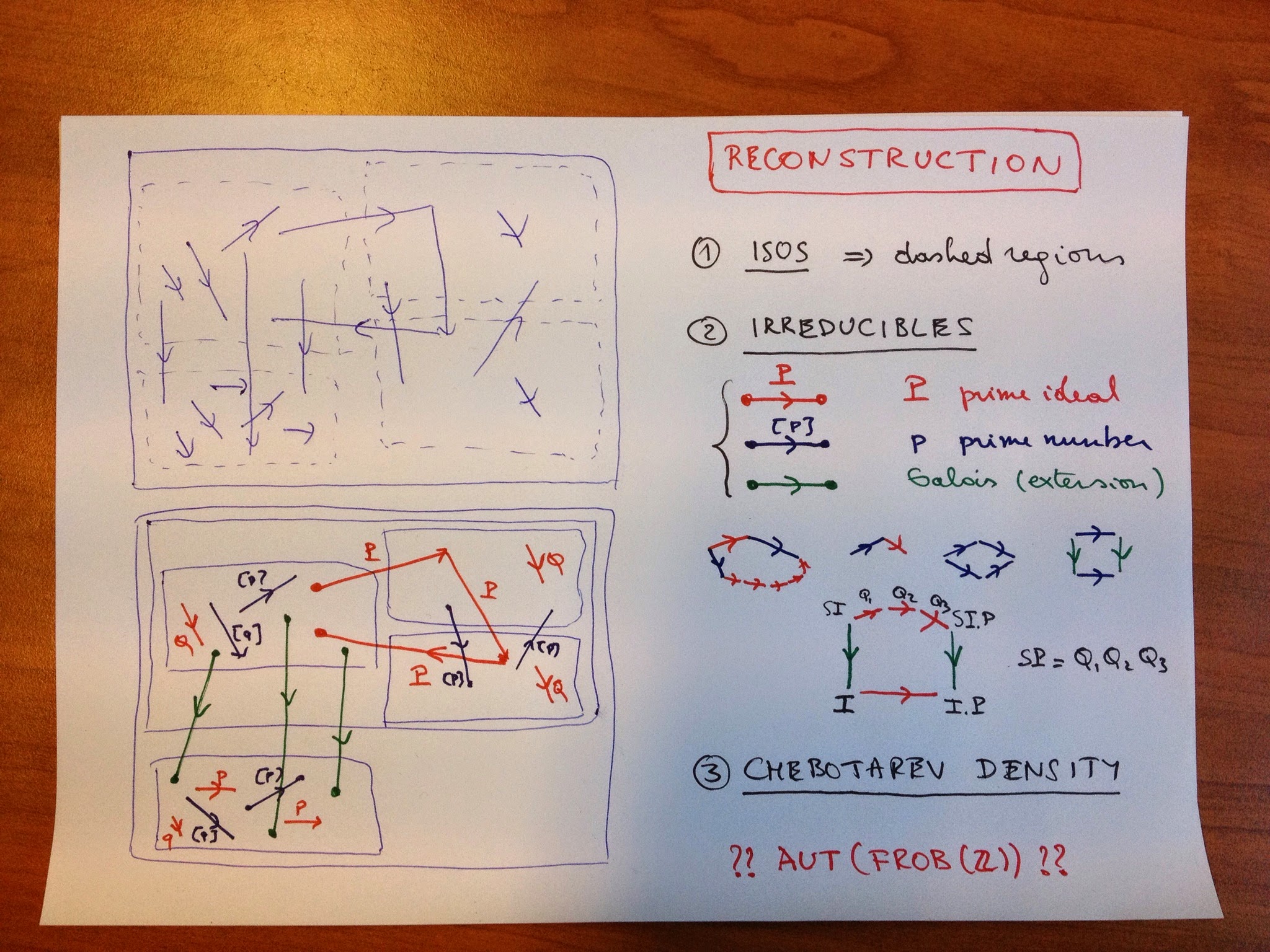
However, in this reconstruction process we are only allowed t use the category structure, so all objects and morphisms are unlabelled (the situation top left) and we want to reconstruct from it the different layers of the Frobenioid (corresponding to the different subfields) and divide all arrows according to their type (situation bottom left).

First we can look at all isomorphisms. They will divide the category in the dashed regions, some of them will be an entire layer (for example for $\mathbb{Q}$) but in general a finite number of these regions will make up the full layer of a subfield (the regions labeled by the elements of the ideal class group).

Another categorical notion we can use are ‘irreducible morphisms’, that is a morphism $f$ which is not an iso but having the property that in each factorisation $f = g \circ h$ either $g$ or $h$ must be an iso. If we remember the different types of morphisms in our Frobenioid we see that the irreducibles come in 3 flavours:

– oRder-maps (Red) : multiplication by a prime ideal $P$ of the ring of integers of the subfield
– froBenius or power-maps (Blue) sendingg a fractional ideal $I$ to $I^p$ for a prime number $p$
– Galois-maps (Green) extending ideals for a subfield $K$ to $K’$ having no intermediate field.

We would like to determine the colour of these irreducibles purely categorical. The idea is that reds have the property that they can be composed with another irreducible (in fact, of power type) such that the composition can again be decomposed in irreducibles and that there is no a priori bound on the number of these terms (this uses the fact that $[p] \circ Q = Q \circ Q \circ … Q \circ [p]$ and that there are infinitely many prime numbers $p$). One checks that compositions of order or Galois maps with irreducibles have factorisation with a bounded number of irreducibles.

The most interesting case is the composition of a Galois map with an order map $P$, this can be decomposed alternatively as order maps in the bigger field followed by a Galois map, the required order maps are the bigger primes $Q_i$ occurring in the decomposition of the extended ideal

\[
S.P = Q_1.Q_2….Q_k \]

but the number $k$ of this decomposition is bounded by the dimension of the bigger field over the smaller one. Summarizing:

– we can determine all the red maps, which will then give us also the different layers
– we can determine the green maps as they move between different layers
– to the remaining blue ones we can even associate their label $[p]$ by the observed property of composition with order maps.

Taking an object in a layer, we get the set of prime ideals of the ring on integers in that field as the set of all red arrows leaving that object unto equivalence (by composing with an isomorphism), so we get the prime spectra $\mathbf{Spec}(S)$.

For a ring-extension  $R \rightarrow S$ we also can recover the cover map $\mathbf{Spec}(S) \rightarrow \mathbf{Spec}(R)$

Indeed, composing the composition of the Galois map with the order-map $P$ and decomposing it alternatively will give us the finite number of prime ideals $Q_i$ of $S$ lying over $P$. That is, we get all splitting behaviour of prime ideals in intermediate field-extensions.

Let $K$ be a Galois subfield of $L$ then we have a way to see how a prime ideals in $\mathbf{Spec}(\mathbb{Z})$ splits, ramifies or remains inert in $K$ and so by Chebotarev density this gives us the dimension of $K$ as well as the Galois group. And, if we could label the prime ideal by a prime number $p$, we could even reconstruct $K$ itself as $K$ is determined once we know all prime numbers which completely split.

The problem i have is that i do not see a categorical way to label the red arrows in $Frob(\mathbb{Z})$ by prime numbers. Mochizuki says we can do this in the proof of Thm 6.4(iii) by using the fact that the $log(p)$ are linearly independent over $\mathbb{Q}$.

This suggests that one might use the ‘Arakelov information’ (that is the archimidean valuations) to do this (the bit i left out so far), but i do not see this in the case of $\mathbb{Q}$ as there is just 1 extra (real) valuation determined by the values of the nonarchimidean valuations.

Probably i am missing something so all sorts of enlightenment re welcome!

Perhaps the ‘hottest’ topic I got involved with on Google+ was Mochizuki’s (claimed) proof of the ABC-conjecture.

Rereading these posts in chronological order shows my changing attitude to this topic, from early skepticism, over attempts to understand at least one pre-IUTeich paper (Frobenioids 1) to a level of belief, to … resignation.

Here’s the first batch of #IUTeich posts (here IUTeich stands for Mochizuki’s ‘Inter Universal Teichmuller theory).

June 12th, 2012

Linked post: ABC conjecture rumor at the Secret Blogging Seminar.

My understanding is that Google+ is for spreading (or debunking) such rumours. Sure would love to have more details!

May 26th, 2013

The Mochizuki craze continues…
Now Ted Nelson claims Mochizuki must be none other than the mysterious Satoshi Nakamoto, inventor of BitCoin.
I’ve seen BitCoin explained in 60 second on YouTube. It would be great if someone did something similar and try to explain inter-universal Teichmuller theory in 60 seconds…

May 27th, 2013

in IUTeich the theta function corresponds to the gaze of the little girl into the “small house”

Yesterday i was hoping for a 60 second introduction to inter-universal Teichmuller theory. Today i learned that Mochizuki himself provided such a thing.

Well, sort of…

In a one-page post he gives an ‘explanation’ of IUTeich via Sokkuri-Animation (Sokkuri being the Japanese for mirror-image). 

IUTeich, he says, should be viewed as a sequence of nested universes, which are represented by ‘houses’ in Sokkuri-Animation.
Galois groups and arithmetic fundamental groups behave as though they are made of a “mysterious substance” and in Sokkuri this “mysterious substance” corresponds to the “mysterious stars” that form the link between the “small” and “large” houses.
And, most importantly, the bridge between these nested universes corresponds to the gaze of the little girl into the “small house”…

Well, that explains everything, i think.

There’s a small image in the post but the link no longer works as the service stopped in january (via Google-translate).

A post at Hacker news identifies the image as coming from the YouTube linked below (2/4/2019 : link lost) and  discovers a connection to the paper titled ‘The ABC Conjecture and the Last Judgment by Giotto’ 

Yesterday i seriously doubted Ted Nelson’s claim that Mochizuki might be the anonymous Hatoshi Nakamoto, designer of BitCoin, having found little or no evidence of CypherPunk-parlance in Mochizuki’s papers…

Today, i’m not that certain any more.

May 28th, 2013

MochizukiDenial

Starting head-on with the 4 papers on inter-universal Teichmuller theory (IUTeich for the fans) is probably not the smartest move to enter Mochizuki-territory.

If you glanced through any of these papers or one of his numerous talks, you’ll know he makes a point of ‘extending’ or even ‘partially dismantling’  scheme theory using the new notion of Frobenioids, which should be some generalisation of Galois categories. 

So if you ever feel like wasting some months trying to figure out what his claimed proof of the ABC-conjecture is all about, a more advisable route might be to start with his two papers on ‘the geometry of Frobenioids’.

Lots of people must have tried that entrance before, and some even started a blog to record their progress as did the person (or persons) behind MochizukiDenial. Here’s the idea:

“Mochizuki deniers by contrast believe that the claim is not serious. They believe that the body of Mochizuki’s work contains neither a proof outline nor ideas powerful enough to resolve the ABC conjecture. We might be wrong. How do we propose to determine whether or not we are. In contrast to Mochizuki boosters on the internet, we will do this by determining what it is that Mochizuki’s papers purport to do. Stay tuned.”

Unfortunately, the project was given up after 2 days and three posts…

Today i tried to acquaint myself with the 126 pages of Frobenioids1 and have a splitting headache because i miss an extra 2Gb RAM to remember the 173 (or more) new concepts he introduces. 

May 29th, 2013

a baby Arithmetic Frobenioid

probably i should start-up a YouTube channel MinuteMochizuki but until i do here’s what i learned today: Alexei Bondal once told me that some Russians start a paper at the end and work their way to the front when needed. Sound advice when approaching M-papers!

So today i did start with the last section ‘Some Motivating Examples’ from Frobenioids1 and worked out what the simplest possible ArithmeticFrobenioid might be, that associated to the integers $\mathbb{Z}$.

Brace yourself here it comes. It is the category $\mathbf{C}$ with objects $(a)$ where $a$ is a strictly positive rational number and morphisms
$(a) \rightarrow (b)$ given by a couple $(n,c)$ where $n$ is a strictly positive integer and $c$ a strictly positive rational number subject to the condition that $a^n$ divides $c.b$ (meaning that the quotient is a strictly positive integer).

Cute (trivial) fact: compositions exist in the sense that
\[
(m,d) \circ (n,c)=(n.m,c^m.d). \]
What makes $\mathbf{C}$ a frobenioid is that it comes with a functor $\mathbf{C} \rightarrow \mathbf{F}$ where $\mathbf{F}$ is the category with one object $*$ and morphisms elements of the noncommutative monoid consisting of all couples $(n,c)$ as before and multiplication as composition above, functor sending all $(a)$ to $*$ and morphisms to corresponding element of the monoid.

Mochizuki proves that we can recover $\mathbf{C}$ from the functor $\mathbf{C} \rightarrow \mathbf{F}$ (look at endomorphism-submonoids of the nc-monoid above) and that $\mathbf{C}$ contains enough info to reconstruct the scheme $\mathbf{Spec}(\mathbb{Z})$ from it (again, use the functor).

Next goal: bring in some Galois categories (tbc)…

May 31st, 2013

MinuteMochizuki 2 : a quadratic arithmetic Frobenioid

Let $m$ be a squarefree number not 1 mod 4 and say you want to recover the classical arithmetic scheme cover $\mathbf{Spec}(\mathbb{Z}[\sqrt{m}])$ onto $\mathbf{Spec}(\mathbb{Z})$ (top left hand corner for m=3).
Prime ideals of $\mathbb{Z}$ may remain prime in $\mathbb{Z}[\sqrt{m}]$ (e.g. (5) and (7)) or split into two prime ideals (e.g. (11)) or ramify (only (2) and (3)), all this governed by the Kronecker symbol.
If it remains prime then the quotient $\mathbb{Z}[\sqrt{m}]/(p)$ is the finite field on $p^2$ elements so has a non-trivial Frobenius morphism, which cannot be lifted to an auto of $\mathbb{Z}[\sqrt{m}]$ to cannot be expressed in scheme language.

For this reason (i think) Mochizuki introduced Frobenioids which are categories allowing one to recover the classical scheme cover but also containing info on the power maps $x \rightarrow x^n$ for all $n$.

In the quadratic case, the objects of the Frobenioid for $\mathbb{Z}[\sqrt{m}]$ is the union of all fractional ideals (that is submodules of $\mathbb{Q}(\sqrt{m})$ of the form $I.q$ where $I$ is an ideal and $q$ non-zero in $\mathbb{Q}(\sqrt{m}))$ and all fractional ideals of $\mathbb{Z}$ (similar defined). Dedekind already knew they correspond to elements of the free Abelian groups on the set of prime ideals and hence have a natural poset-structure.

Now, there are monoid actions on these two posets, giving another set of arrows (for fractional ideals of $\mathbb{Z}[\sqrt{m}]$ the black arrows indicate the poset and the red arrow is the action. Now, the morphisms in the Frobenioid $\mathbf{C}(m)$ are all compositions of an action arrow followed by a poset-arrow (the green ones in the $\mathbb{Z}[\sqrt{m}]$ part, the red ones in the $\mathbb{Z}$-part. Then there is a third set of arrows encoding the Galois-covering info (the black arrows between the two parts). Again, one verifies that compositions exist.

A very special case of Mochizuki’s first Frobenioid paper is that $\mathbf{C}(m)$ contains enough info to recover the scheme cover and even the quadratic field $\mathbb{Q}(\sqrt{m})$. That is, if $\mathbf{C}(m)$ is equivalent to another such one $\mathbf{C}(m’)$ then $m=m’$. Also note that $\mathbf{C}(m)$ contains info on all power maps, so we have somehow ‘lifted’ the Frobenius-maps from the quotients to $\mathbb{Z}[\sqrt{m}]$ at the expense of ‘partially dismantling scheme theory’ (M’s words).

Another neat fact about $\mathbf{C}(m)$ is that all arrows are epimorphisms (compare this to groupoids where all morphisms are isomorphisms). Of course, this only becomes important for more complicated Galois-settings, ideally for the algebraic closure of $\mathbb{Q}$.

June 1st, 2013

Should I stay or should I blog now?

+Alex Nelson commented on +John Baez reshare of my last post on Mochizuki’s Frobenioids:
 
“I just wish he’d blog these, to make it a wee bit easier to read…and print out…”

Valid point, so i did spend some time to make blog-versions of my two G+ posts on this, the last one is linked below, the first one is here (2/4/2019 : lost post).

I’m not sure whether i should continue with this cross-posting. I kinda liked the quick-and-dirty approach of instant-uploading snaps-shots of doodles here. Writing a blogpost  takes more time.

Let me know if it does make a difference to you.

June 3rd, 2013

Mochizuki’s menagerie of morphisms

After zillions of definitions, Mochizuki almost shows empathy with the reader (on page 26 of Frobenioids1) and remarks  that it may be useful to draw a “Chart of Types of Morphisms in a Frobenioid”  (and does this on page 124).

Extremely useful indeed. Try to figure out what a morphism of Frobenius-type might be. It starts like this: it is an LB-invertible base-isomorphism. An LB-invertible map itself is a co-angular and isometric map. A co-angular map itself is defined by the property that for any factorization aoboc of it, where a is linear, b is an isometric pre-step and either a or c are base-isomorphisms, it follows that b is an isomorphism. A pre-step itself is …. etc.etc.

Today i tried to work out what all this means in the case of an arithmetic Frobenioid. Recall that this is a category with objects the elements of layers of posets, each layer (meant to represent the ‘dismantled’ prime-spectrum of a ring of integers $R$ in a number field $K$) the set of fractional ideals in the number field. In each layer we have operations of three types

– Frobenius-type : sending a fractional ideal $I$ to an n-th power $I^n$ (the blue morphisms)
– Poset-type : given by multiplying $I$ with an ideal $K$ of $R$ (the red morphisms, the ‘steps’ in M-parlance)
– Isomorphisms (the blacks, ‘isometric pre-steps’ according to M) which are either isos of fractional ideals (given by multiplying with a non-zero element $q$ of $K$) or Galois action maps on fractional ideals.

The relevant operation between different layers is that of extension of fractional ideals. So, let $\sigma : R \rightarrow S$ be a ring-map induced by a field-iso on $L$, the number-field of $S$, then this operation sends a fractional ideal $J$ in $K$ to the extended fractional ideal $S.\sigma(J)$ in $L$.

What Mochizuki shows is that any arrow in the arithmetic Frobenioid has an essentially unique factorisation into these four types of morphisms (essentially meaning unto irrelevant  isos trown in at one place and compensated by the inverse at the next place).

Let’s work this out for the baby arithmetic Frobenioid corresponding to the integers.

Objects correspond to strictly positive rational numbers $a$, and morphisms are of the form $\phi=(n,q,z) : a \rightarrow b$  where $n$ and $z$ are strictly positive integers and $q$ a strictly positive rational number satisfying $a^n.z=b.q$.

This map can then be factored as a Frobenius-type map $(n,1,1)$ sending $a$ to $a^n$, followed by a poset-map $(1,1,z)$ sending $a^n$ to $a^n.z$ followed by an isomorphism $(1,q^{-1},1)$ sending $a^n.z$ to $a^n.z.q^{-1}=b$.

These different types of morphisms will become important when we want to reconstruct the arithmetic schemes (and covers) from the category structure of the Frobenioid. The essential trick will be to classify and distinguish the irreducible morphisms which are non-isomorphisms phi such that in any factorisation $\phi = \alpha \circ \beta$, either $\alpha$ or $\beta$ must be an isomorphism. (tbc)