Skip to content →

Category: math

Bourbaki and Dema, two remarks

Published February 26, 2024 by lieven

While this blog is still online, I might as well correct, and add to, previous posts.

Later this week new Twenty One Pilots material is expected, so this might be a good time to add some remarks to a series of posts I ran last summer, trying to find a connection between Dema-lore and the actual history of the Bourbaki group. Here are links to these posts:

In the post “9 Bourbaki founding members, really?” I questioned Wikipedia’s assertion that there were exactly nine founding members of Nicolas Bourbaki:

I still stand by the arguments given in that post, but my opinion on this is completely irrelevant. What matters is who the Bourbaki-gang themself deemed worthy to attach their names to their first publication ‘Theorie des Ensembles’ (1939).

But wait, wasn’t the whole point of choosing the name Nicolas Bourbaki for their collective that the actual authors of the books should remain anonymous?

Right, but then I found this strange document in the Bourbaki Archives : awms_001, a preliminary version of the first two chapters of ‘Theorie des Ensembles’ written by Andre Weil and annotated by Rene de Possel. Here’s the title page:

Next to N. Bourbaki we see nine capital letters: M.D.D.D.E.C.C.C.W corresponding to nine AW-approved founding members of Bourbaki: Mandelbrojt, Delsarte, De Possel, Dieudonne, Ehresmann, Chevalley, Coulomb, Cartan and Weil!

What may freak out the Clique is the similarity between the diagram to the left of the title, and the canonical depiction of the nine Bishops of Dema (at the center of the map of Dema) or the cover of the Blurryface album:




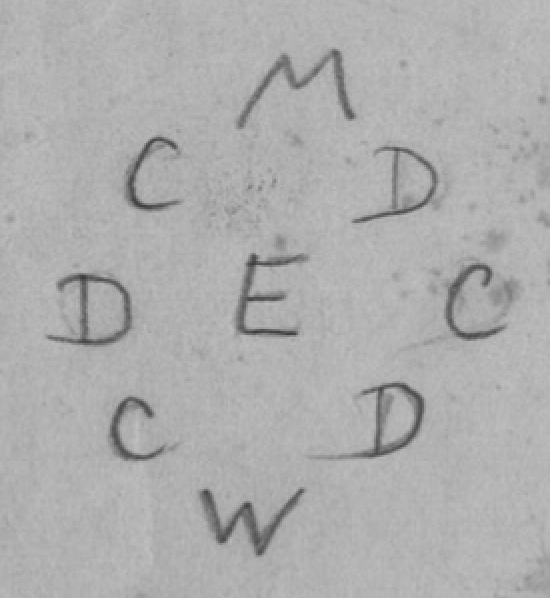
In the Photoshop mysteries post I explained why Mandelbrojt and Weil might have been drawn in opposition to each other, but I am unaware of a similar conflict between either of the three C’s (Cartan, Coulomb and Chevalley) and the three D’s (Delsarte, De Possel and Dieudonne).

So, I’ll have to leave the identification of the nine Bourbaki founding members with the nine Dema Bishops as a riddle for another post.

The second remark concerns the post Where’s Bourbaki’s Dema?.

In that post I briefly suggested that DEMA might stand for DEutscher MAthematiker (German Mathematicians), and hinted at the group of people around David Hilbert, Emil Artin and Emmy Noether, but discarded this as “one can hardly argue that there was a self-destructive attitude (like Vialism) present among that group, quite the opposite”.

At the time, I didn’t know about Deutsche Mathematik, a mathematics journal founded in 1936 by Ludwig Bieberbach and Theodor Vahlen.



Deutsche Mathematik is also the name of a movement closely associated with the journal whose aim was to promote “German mathematics” and eliminate “Jewish influence” in mathematics. More about Deutsche Mathematik can be found on this page, where these eight mathematicians are mentioned in connection with it:

Perhaps one can add to this list:

Whether DEutsche MAthematik stands for DEMA, and which of these German mathematicians were its nine bishops might be the topic of another post. First I’ll have to read through Sanford Segal’s Mathematicians under the Nazis.

Added February 29th:

The long awaited new song has now surfaced:

I’ve only watched it once, but couldn’t miss the line “I fly by the dangerous bend symbol“.

Didn’t we all fly by them in our first readings of Bourbaki…

(Fortunately the clique already spotted that reference).

No intention to freak out clikkies any further, but in the aforementioned Weil draft of ‘Theorie des Ensembles’ they still used this precursor to the dangerous bend symbol

Skeletons anyone?

Comments closed

Grothendieck’s gribouillis (6)

Published October 2, 2023 by lieven

After the death of Grothendieck in November 2014, about 30.000 pages of his writings were found in Lasserre.



Since then I’ve been trying to follow what happened to them:

So, what’s new?

Well, finally we have closure!

Last Friday, Grothendieck’s children donated the 30.000 Laserre pages to the Bibliotheque Nationale de France.

Via Des manuscrits inédits du génie des maths Grothendieck entrent à la BnF (and Google-translate):

“The singularity of these manuscripts is that they “cover many areas at the same time” to form “a whole, a + cathedral work +, with undeniable literary qualities”, analyzes Jocelyn Monchamp, curator in the manuscripts department of the BnF.

More than in “Récoltes et semailles”, very autobiographical, the author is “in a metaphysical retreat”, explains the curator, who has been going through the texts with passion for a month. A long-term task as the writing, in fountain pen, is dense and difficult to decipher. “I got used to it… And the advantage for us was that the author had methodically paginated and dated the texts.” One of the parts, entitled “Structures of the psyche”, a book of enigmatic diagrams translating psychology into algebraic language. In another, “The Problem of Evil”, he unfolds over 15,000 pages metaphysical meditations and thoughts on Satan. We sense a man “caught up by the ghosts of his past”, with an adolescence marked by the Shoah, underlines Johanna Grothendieck whose grandfather, a Russian Jew who fled Germany during the war, died at Auschwitz.

The deciphering work will take a long time to understand everything this genius wanted to say.

On Friday, the collection joined the manuscripts department of the Richelieu site, the historic cradle of the BnF, alongside the writings of Pierre and Marie Curie and Louis Pasteur. It will only be viewable by researchers.“This is a unique testimony in the history of science in the 20th century, of major importance for research,” believes Jocelyn Monchamp.

During the ceremony, one of the volumes was placed in a glass case next to a manuscript by the ancient Greek mathematician Euclid.”

Probably, the recent publication of Récoltes et Semailles clinched the deal.

Also, it is unclear at this moment whether the Istituto Grothendieck, which harbours The centre for Grothendieck studies coordinated by Mateo Carmona (see this post) played a role in the decision making, nor what role the Centre will play in the further studies of Grothendieck’s gribouillis.

For other coverage on this, see Hermit ‘scribblings’ of eccentric French math genius unveiled.

3 Comments

A question of loyalty

Published September 29, 2023 by lieven

On the island of two truths, statements are either false (truth-value $0$), Q-true (value $Q$) or K-true (value $K$).

The King and Queen of the island have an opinion on all statements which may differ from their actual truth-value. We say that the Queen believes a statement $p$ is she assigns value $Q$ to it, and that she knows $p$ is she believes $p$ and the actual truth-value of $p$ is indeed $Q$. Similarly for the King, replacing $Q$’s by $K$’s.

All other inhabitants of the island are loyal to the Queen, or to the King, or to both. This means that they agree with the Queen (or King, or both) on all statements they have an opinion on. Two inhabitants are said to be loyal to each other if they agree on all statements they both have an opinion of.

Last time we saw that Queen and King agree on all statements one of them believes to be false, as well as the negation of such statements. This raised the question:

Are the King and Queen loyal to each other? That is, do Queen and King agree on all statements?

We cannot resolve this issue without the information Oscar was able to extract from Pointex in Karin Cvetko-Vah‘s post Pointex:

“Oscar was determined to get some more information. “Could you at least tell me whether the queen and the king know that they’re loyal to themselves?” he asked.
“Well, of course they know that!” replied Pointex.
“You said that a proposition can be Q-TRUE, K-TRUE or FALSE,” Oscar said.
“Yes, of course. What else!” replied Pointex as he threw the cap high up.
“Well, you also said that each native was loyal either to the queen or to the king. I was just wondering … Assume that A is loyal to the queen. Then what is the truth value of the statement: A is loyal to the queen?”
“Q, of course,” answered Pointex as he threw the cap up again.
“And what if A is not loyal to the queen? What is then the truth value of the statement: A is loyal to the queen?”
He barely finished his question as something fell over his face and covered his eyes. It was the funny cap.
“Thanx,” said Pointex as Oscar handed him the cap. “The value is 0, of course.”
“Can the truth value of the statement: ‘A is loyal to the queen’ be K in any case?”
“Well, what do you think? Of course not! What a ridiculous thing to ask!” replied Pointex.”

Puzzle : Show that Queen and King are not loyal to each other, that is, there are statements on which they do not agree.



Solution : ‘The King is loyal to the Queen’ must have actual truth-value $0$ or $Q$, and the sentence ‘The Queen is loyal to the King’ must have actual truth-value $0$ or $K$. But both these sentences are the same as the sentence ‘The Queen and King are loyal to each other’ and as this sentence can have only one truth-value, it must have value $0$ so the statement is false.

Note that we didn’t produce a specific statement on which the Queen and King disagree. Can you find one?

Comments closed