Skip to content →

Category: groups

Extending McKay’s E8 graph?

Published January 25, 2018 by lieven

If you take two Fischer involutions in the monster (elements of conjugacy class 2A) and multiply them, the resulting element surprisingly belongs to one of just 9 conjugacy classes:

1A,2A,2B,3A,3C,4A,4B,5A or 6A

The orders of these elements are exactly the dimensions of the fundamental root for the extended $E_8$ Dynkin diagram.

This is the content of John McKay’s E(8)-observation : there should be a precise relation between the nodes of the extended Dynkin diagram and these 9 conjugacy classes in such a way that the order of the class corresponds to the component of the fundamental root. More precisely, one conjectures the following correspondence:

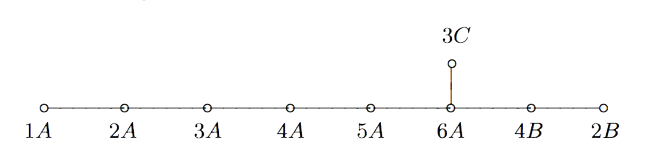
John Duncan found such a connection by considering carefully the corresponding moonshine groups and their inter-relation. For more on this, look at the old post E8 from moonshine groups. The extended Dynkin diagram with these moonshine groups as vertices is:

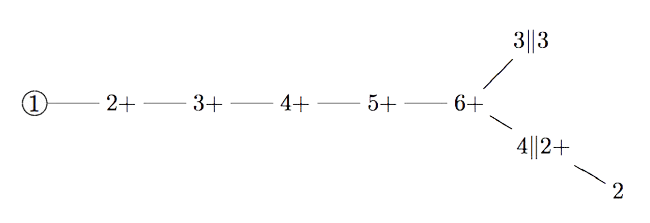
Duncan does this by assigning numbers to moonshine groups: the dimension is the order of the corresponding monster element and the valency is one more than the copies of $C_2$ generated by the Atkin-Lehner involutions in the moonshine group.

One might ask whether there is a graph on all 171 moonshine groups, compatible with the valencies of every vertex.

Now, even for the 9 groups in McKay’s question, the valencies do not determine the graph uniquely and Duncan proceeds with an ad hoc condition on the edges.

There is a partition on the 9 groups by the property whether or not the index of the intersection with $\Gamma_0(2)$ is at most two. Then Duncan declares that there cannot be an edge between two groups belonging to the same class.

His motivation for this property comes from classical McKay-correspondence for the binary icosahedral group (where the vertices correspond to simple representations $S$, and the edges from $S$ to factors of $S \otimes V_2$, where $V_2$ is the restriction of the standard $2$-dimensional simple for $SU(2)$).

Of the $9$ simples there are only $4$ faithful ones, $5$ come from simples of $A_5$. Because $\Gamma_0(2)$ is a subgroup of the modular group of index 2, he then views $\Gamma_0(2)$ as similar to the subgroup $A_5$ in the binary icosahedral group, and declares a moonshine group to be faithful if its index in the intersection with $\Gamma_0(2)$ is at most two.

One might ask whether there is another, more natural, definition for having an edge (or multiple ones) between arbitrary moonshine groups.

And, what is the full graph on the 171 groups?

Comments closed

the moonshine picture – at last

Published January 23, 2018 by lieven

The monstrous moonshine picture is the subgraph of Conway’s big picture consisting of all lattices needed to describe the 171 moonshine groups.

It consists of:

– exactly 218 vertices (that is, lattices), out of which

– 97 are number-lattices (that is of the form $M$ with $M$ a positive integer), and

– 121 are proper number-like lattices (that is of the form $M \frac{g}{h}$ with $M$ a positive integer, $h$ a divisor of $24$ and $1 \leq g \leq h$ with $(g,h)=1$).

The $97$ number lattices are closed under taking divisors, and the corresponding Hasse diagram has the following shape

Here, number-lattices have the same colour if they have the same local structure in the moonshine picture (that is, have a similar neighbourhood of proper number-like lattices).

There are 7 different types of local behaviour:

The white numbered lattices have no proper number-like neighbours in the picture.

The yellow number lattices (2,10,14,18,22,26,32,34,40,68,80,88,90,112,126,144,180,208 = 2M) have local structure

\[
\xymatrix{M \ar@{-}[r] & \color{yellow}{2M} \ar@{-}[r] & M \frac{1}{2}} \]

which involves all $2$-nd (square) roots of unity centered at the lattice.

The green number lattices (3,15,21,39,57,93,96,120 = 3M) have local structure

\[
\xymatrix{& M \ar@[red]@{-}[d] & \\ M \frac{1}{3} \ar@[red]@{-}[r] & \color{green}{3M} \ar@[red]@{-}[r] & M \frac{2}{3}} \]

which involve all $3$-rd roots of unity centered at the lattice.

The blue number lattices (4,16,20,28,36,44,52,56,72,104 = 4M) have as local structure

\[
\xymatrix{M \frac{1}{2} \ar@{-}[d] & & M \frac{1}{4} \ar@{-}[d] \\
2M \ar@{-}[r] & \color{blue}{4M} \ar@{-}[r] & 2M \frac{1}{2} \ar@{-}[d] \\
M \ar@{-}[u] & & M \frac{3}{4}} \]

and involve the $2$-nd and $4$-th root of unity centered at the lattice.

The purple number lattices (6,30,42,48,60 = 6M) have local structure

\[
\xymatrix{& M \frac{1}{3} \ar@[red]@{-}[d] & 2M \frac{1}{3} & M \frac{1}{6} \ar@[red]@{-}[d] & \\
M \ar@[red]@{-}[r] & 3M \ar@{-}[r] \ar@[red]@{-}[d] & \color{purple}{6M} \ar@{-}[r] \ar@[red]@{-}[u] \ar@[red]@{-}[d] & 3M \frac{1}{2} \ar@[red]@{-}[r] \ar@[red]@{-}[d] & M \frac{5}{6} \\
& M \frac{2}{3} & 2M \frac{2}{3} & M \frac{1}{2} & } \]

and involve all $2$-nd, $3$-rd and $6$-th roots of unity centered at the lattice.

The unique brown number lattice 8 has local structure

\[
\xymatrix{& & 1 \frac{1}{4} \ar@{-}[d] & & 1 \frac{1}{8} \ar@{-}[d] & \\
& 1 \frac{1}{2} \ar@{-}[d] & 2 \frac{1}{2} \ar@{-}[r] \ar@{-}[d] & 1 \frac{3}{4} & 2 \frac{1}{4} \ar@{-}[r] & 1 \frac{5}{8} \\
1 \ar@{-}[r] & 2 \ar@{-}[r] & 4 \ar@{-}[r] & \color{brown}{8} \ar@{-}[r] & 4 \frac{1}{2} \ar@{-}[d] \ar@{-}[u] & \\
& & & 1 \frac{7}{8} \ar@{-}[r] & 2 \frac{3}{4} \ar@{-}[r] & 1 \frac{3}{8}} \]

which involves all $2$-nd, $4$-th and $8$-th roots of unity centered at $8$.

Finally, the local structure for the central red lattices $12,24 = 12M$ is

\[
\xymatrix{
M \frac{1}{12} \ar@[red]@{-}[dr] & M \frac{5}{12} \ar@[red]@{-}[d] & M \frac{3}{4} \ar@[red]@{-}[dl] & & M \frac{1}{6} \ar@[red]@{-}[dr] & M \frac{1}{2} \ar@[red]@{-}[d] & M \frac{5}{6} \ar@[red]@{-}[dl] \\
& 3M \frac{1}{4} \ar@{-}[dr] & 2M \frac{1}{6} \ar@[red]@{-}[d] & 4M \frac{1}{3} \ar@[red]@{-}[d] & 2M \frac{1}{3} \ar@[red]@{-}[d] & 3M \frac{1}{2} \ar@{-}[dl] & \\
& 2M \frac{1}{2} \ar@[red]@{-}[r] & 6M \frac{1}{2} \ar@{-}[dl] \ar@[red]@{-}[d] \ar@{-}[r] & \color{red}{12M} \ar@[red]@{-}[d] \ar@{-}[r] & 6M \ar@[red]@{-}[d] \ar@{-}[dr] \ar@[red]@{-}[r] & 2M & \\
& 3M \frac{3}{4} \ar@[red]@{-}[dl] \ar@[red]@{-}[d] \ar@[red]@{-}[dr] & 2M \frac{5}{6} & 4M \frac{2}{3} & 2M \frac{2}{3} & 3M \ar@[red]@{-}[dl] \ar@[red]@{-}[d] \ar@[red]@{-}[dr] & \\
M \frac{1}{4} & M \frac{7}{12} & M \frac{11}{12} & & M \frac{1}{3} & M \frac{2}{3} & M}
\]

It involves all $2$-nd, $3$-rd, $4$-th, $6$-th and $12$-th roots of unity with center $12M$.

No doubt this will be relevant in connecting moonshine with non-commutative geometry and issues of replicability as in Plazas’ paper Noncommutative Geometry of Groups like $\Gamma_0(N)$.

Another of my pet follow-up projects is to determine whether or not the monster group $\mathbb{M}$ dictates the shape of the moonshine picture.

That is, can one recover the 97 number lattices and their partition in 7 families starting from the set of element orders of $\mathbb{M}$, applying some set of simple rules?

One of these rules will follow from the two equivalent notations for lattices, and the two different sets of roots of unities centered at a given lattice. This will imply that if a number lattice belongs to a given family, certain divisors and multiples of it must belong to related families.

If this works out, it may be a first step towards a possibly new understanding of moonshine.

Comments closed

a non-commutative Jack Daniels problem

Published January 20, 2018 by lieven

At a seminar at the College de France in 1975, Tits wrote down the order of the monster group

\[
\# \mathbb{M} = 2^{46}.3^{20}.5^9.7^6.11^2.13^3.17·19·23·29·31·41·47·59·71 \]

Andrew Ogg, who attended the talk, noticed that the prime divisors are precisely the primes $p$ for which the characteristic $p$ super-singular $j$-invariants are all defined over $\mathbb{F}_p$.

Here’s Ogg’s paper on this: Automorphismes de courbes modulaires, Séminaire Delange-Pisot-Poitou. Théorie des nombres, tome 16, no 1 (1974-1975).

Ogg offered a bottle of Jack Daniels for an explanation of this coincidence.

Even Richard Borcherds didn’t claim the bottle of Jack Daniels, though his proof of the monstrous moonshine conjecture is believed to be the best explanation, at present.

A few years ago, John Duncan and Ken Ono posted a paper “The Jack Daniels Problem”, in which they prove that monstrous moonshine implies that if $p$ is not one of Ogg’s primes it cannot be a divisor of $\# \mathbb{M}$. However, the other implication remains mysterious.

Duncan and Ono say:

“This discussion does not prove that every $p ∈ \text{Ogg}$ divides $\# \mathbb{M}$. It merely explains how the first principles of moonshine suggest this implication. Monstrous moonshine is the proof. Does this then provide a completely satisfactory solution to Ogg’s problem? Maybe or maybe not. Perhaps someone will one day furnish a map from the characteristic $p$ supersingular $j$-invariants to elements of order $p$ where the group structure of $\mathbb{M}$ is apparent.”

I don’t know whether they claimed the bottle, anyway.

But then, what is the non-commutative Jack Daniels Problem?

A footnote on the first page of Conway and Norton’s ‘Monstrous Moonshine’ paper says:

“Very recently, A. Pizer has shown these primes are the only ones that satisfy a certain conjecture of Hecke from 1936 relating modular forms of weight $2$ to quaternion algebra theta-series.”

Pizer’s paper is “A note on a conjecture of Hecke”.

Maybe there’s a connection between monstrous moonshine and the arithmetic of integral quaternion algebras. Some hints:

The commutation relations in the Big Picture are reminiscent of the meta-commutation relations for Hurwitz quaternions, originally due to Conway in his booklet on Quaternions and Octonions.

The fact that the $p$-tree in the Big Picture has valency $p+1$ comes from the fact that the Brauer-Severi of $M_2(\mathbb{F}_p)$ is $\mathbb{P}^1_{\mathbb{F}_p}$. In fact, the Big Picture should be related to the Brauer-Severi scheme of $M_2(\mathbb{Z})$.

Then, there’s Jorge Plazas claiming that Connes-Marcolli’s $GL_2$-system might be related to moonshine.

One of the first things I’ll do when I return is to run to the library and get our copy of Shimura’s ‘Introduction to the arithmetic theory of automorphic functions’.

Btw. the bottle in the title image is not a Jack Daniels but the remains of a bottle of Ricard, because I’m still in the French mountains.

Comments closed