Before I'm bogged down by the changes let me
return to the snortGO
puzzle. Recall that in snortGO black and white take
turns in placing a Go-stone on the board respecting the rule that no
stones of opposite colour may be adjacent. Javier is right that snortGo
with an empty starting board having an odd number of rows and columns is
a first player's win (place your first stone on the central spot and
respond to your opponent's moves by reflecting them along the
center).
Still, one can compose realistic end-game problems (as
in the previous snortGo post where the problem was : prove that the position is a first
player's win and indicate a winning move for both black and white).
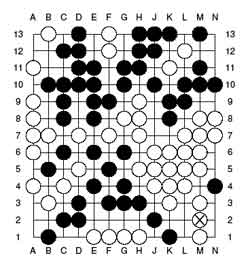
To start the analysis let us remove all spots which are unavailable for
both players (as depicted in the top picture). Some of the remaining
spots are available to just one player (the central free spots and the
two in the top left corner). One counts that black has 5 such central
spots and white 4 (including the top left corner). So, all the genuine
action is happening in the three remaining corner regions for which one
can calculate the exact value following the rules of combinatorial game
theory where bLack is playing Left and white Right (so the free
spots for black add up to +5 whereas those for white add up to -4). It
is pretty easy to work out the exact values of the corner subgames
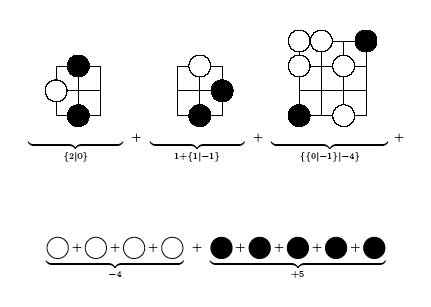
To find the value of the total game we have to sum up these
values which can either be done by hand (use this and this to get
started and use the inductive rule $G+H = \\{ G^L+H,G+H^L \\vert
G^R+H,G+H^R \\}$) or using combinatorial game suite to
verify that this sum is equal to $\\{ \\{ 3 \\vert 2 \\} \\vert -1 \\}$
which is a fuzzy game (that is, confused with zero or a first
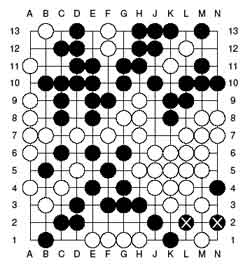
player's win). To find the actual winning moves just try out the
Left (bLack) and Right (white) options in the corner games to find out
that there is a unique winning move for white and there are just 2
winning moves for bLack, all indicated in the pictures below.