featured – Page 20 – neverendingbooks

Hexagonal Moonshine (2)

Published July 11, 2007 by lieven

Delving into finite dimensional representations of the modular group $\Gamma = PSL_2(\mathbb{Z}) $ it is perhaps not too surprising to discover numerical connections with modular functions. Here, one such strange observation and a possible explanation.

Using the _fact_ that the modular group $\Gamma = PSL_2(\mathbb{Z}) $ is the free group product $C_2 \ast C_3 $ it is fairly easy to see that the variety of all n-dimensional representations $\mathbf{rep}_n~\Gamma $ is smooth (though it contains several connected components). Some of these components will contain simple representations, some will not. Anyway, we are not interested in all n-dimensional representations but in the isomorphism classes of such representations. The best algebraic approximation to this problem is by studying the quotient varieties

$\mathbf{iss}_n~\Gamma = \mathbf{rep}_n~\Gamma // GL(n) $

under the action of $GL(n) $ by basechange. Geometric invariant theory tells us that the points of this quotient variety correspond to isoclasses of semi-simple n-dimensional representations (whence the notation $\mathbf{iss}_n $). Again, these quotient varieties split into several connected components, some of which will have an open subset of points corresponding to simple representations.

It is a natural idea to compute the codimension of subvariety of proper semi-simples in the component of maximal dimension containing simple representations. _M-geometry_ allows you to reduce such calculation to quiver-problems. Anyway, if one does this for small values of n one obtains the following sequence of codimension-numbers (starting with $n=1 $

0,1,1,1,1,3,1,3,3,3,3,5,3,5,5,5,5,7,5,7,…

which doesnt seem too exciting before you feed it to Sloan’s integer sequences encyclopedia when one discovers that it is precisely sequence A063195 which gives the dimensions of weight 2n _cuspidal newforms_
for $\Gamma_0(6) $…

The optimistic “moonshine”-interpretation of this might be that these newforms can be viewed somehow as functions on the varieties of finite dimensional $\Gamma $-representations having the property that they pick out generic simple representations as their non-zeroes.

Be that as it may (one never knows in these matters), here a more down-to-earth explanation. The sequence A063195 obviously has a 6-periodicity behaviour so it suffices to understand why the codimension-sequence should have a similar feature (modulo computing the first few terms of it and observing the coincidence with the first few terms of A063195).

The modular group has exactly 6 one-dimensional representations and if one calculates their clan as in hexagonal moonshine (1) one obtains the hexagonal quiver

[tex]\xymatrix{& \vtx{S_1} \ar@/^/[dl] \ar@/^/[dr] & \\ \vtx{S_6} \ar@/^/[ur] \ar@/^/[d] & & \vtx{S_2} \ar@/^/[ul] \ar@/^/[d] \\ \vtx{S_5} \ar@/^/[u] \ar@/^/[dr] & & \vtx{S_3} \ar@/^/[u] \ar@/^/[dl] \\ & \vtx{S_4} \ar@/^/[ur] \ar@/^/[ul] & }[/tex]

M-geometry tells us that this clan contains enough information to determine the components of $\mathbf{rep}_n~\Gamma $ that contain simple representations. They correspond to dimension-vectors of this hexagonal quiver, say

$~(a_1,a_2,a_3,a_4,a_5,a_6) $

such that $a_i \leq a_{i-1}+a_{i+1} $. Moreover, the component is of maximal dimension if the components $a_i $ are evenly spread over the six vertices.
This then explains that the codimension sequence we are interested in must satisfy 6-periodicity.

Reference

This post corrects the erroneous statement made in math.AG/0610587 that the codimension sequence are the dimensions of weight 2n modular forms. The day the paper hit the arXiv I informed the author of the mistakes he made and told him how they could be corrected. Having waited 9 months I’ve given up hope that a revision/correction is imminent.

Farey codes

Published July 1, 2007 by lieven

John Farey (1766-1826) was a geologist of sorts. Eyles, quoted on the math-biographies site described his geological work as

“As a geologist Farey is entitled to respect for the work which he carried out himself, although it has scarcely been noticed in the standard histories of geology.”

That we still remember his name after 200 years is due to a short letter he wrote in 1816 to the editor of the Philosophical Magazine

“On a curious Property of vulgar Fractions.
By Mr. J. Farey, Sen. To Mr. Tilloch

Sir. – On examining lately, some very curious and elaborate Tables of “Complete decimal Quotients,” calculated by Henry Goodwyn, Esq. of Blackheath, of which he has printed a copious specimen, for private circulation among curious and practical calculators, preparatory to the printing of the whole of these useful Tables, if sufficient encouragement, either public or individual, should appear to warrant such a step: I was fortunate while so doing, to deduce from them the following general property; viz.

If all the possible vulgar fractions of different values, whose greatest denominator (when in their lowest terms) does not exceed any given number, be arranged in the order of their values, or quotients; then if both the numerator and the denominator of any fraction therein, be added to the numerator and the denominator, respectively, of the fraction next but one to it (on either side), the sums will give the fraction next to it; although, perhaps, not in its lowest terms.

For example, if 5 be the greatest denominator given; then are all the possible fractions, when arranged, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, and 4/5; taking 1/3, as the given fraction, we have (1+1)/(5+3) = 2/8 = 1/4 the next smaller fraction than 1/3; or (1+1)/(3+2) = 2/5, the next larger fraction to 1/3. Again, if 99 be the largest denominator, then, in a part of the arranged Table, we should have 15/52, 28/97, 13/45, 24/83, 11/38, &c.; and if the third of these fractions be given, we have (15+13)/(52+45) = 28/97 the second: or (13+11)/(45+38) = 24/83 the fourth of them: and so in all the other cases.

I am not acquainted, whether this curious property of vulgar fractions has been before pointed out?; or whether it may admit of any easy or general demonstration?; which are points on which I should be glad to learn the sentiments of some of your mathematical readers; and am

Sir, Your obedient humble servant,
J. Farey. Howland-street.”

So, if we interpolate “childish addition of fractions” $\frac{a}{b} \oplus \frac{c}{d} = \frac{a+c}{b+d} $ and start with the numbers $0 = \frac{0}{1} $ and $\infty = \frac{1}{0} $ we get the binary Farey-tree above. For a fixed natural number n, if we stop the interpolation whenever the denominator of the fraction would become larger than n and order the obtained fractions (smaller or equal to one) we get the Farey sequence F(n). For example, if n=3 we start with the sequence $ \frac{0}{1},\frac{1}{1} $. The next step we get $\frac{0}{1},\frac{1}{2},\frac{1}{1} $ and the next step gives

$\frac{0}{1},\frac{1}{3},\frac{1}{2},\frac{2}{3},\frac{1}{1} $

and as all the denomnators of childish addition on two consecutive fractions will be larger than 3, the above sequence is F(3). A remarkable feature of the series F(n) is that if $\frac{a}{b} $ and $\frac{c}{d} $ are consecutive terms in F(n), then

$det \begin{bmatrix} a & c \\\ b & d \end{bmatrix} = -1 $

and so these two fractions are the endpoints of an even geodesic in the Dedekind tessellation.

A generalized Farey series is an ordered collection of fractions $\infty,x_0,x_1,\cdots,x_n,\infty $ such that $x_0 $ and $x_n $ are integers and some $x_i=0 $. Moreover, writing $x_i = \frac{a_i}{b_i} $ we have that

$det \begin{bmatrix} a_i & a_{i+1} \\\ b_i & b_{i+1} \end{bmatrix} = -1 $

A Farey code is a generalized Farey sequence consisting of all the vertices of a special polygon that lie in $\mathbb{R} \cup \{ \infty \} $ together with side-pairing information. If two consecutive terms are such that the complete geodesic between $x_i $ and $x_{i+1} $ consists of two sides of the polygon which are paired we denote this fact by
[tex]\xymatrix{x_i \ar@{-}[r]_{\circ} & x_{i+1}}[/tex]. If they are the endpoints of two odd sides of the polygon which are paired we denote this by [tex]\xymatrix{x_i \ar@{-}[r]_{\bullet} & x_{i+1}}[/tex]. Finally, if they are the endpoints of a free side which is paired to another free side determined by $x_j $ and $x_{j+1} $ we denote this fact by marking both edges [tex]\xymatrix{x_i \ar@{-}[r]_{k} & x_{i+1}}[/tex] and [tex]\xymatrix{x_j \ar@{-}[r]_{k} & x_{j+1}}[/tex] with the same number.

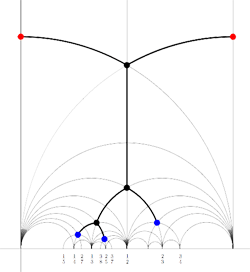
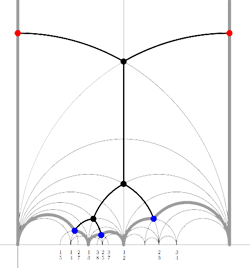
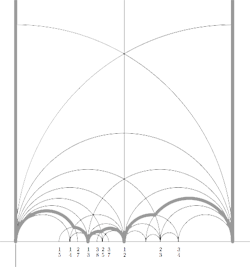
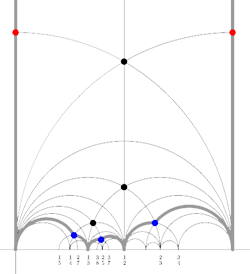
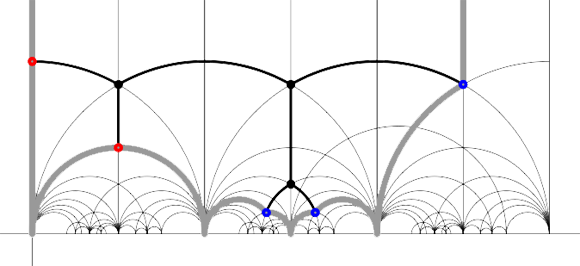
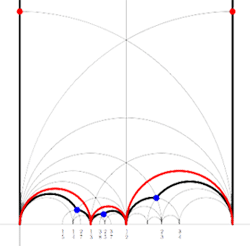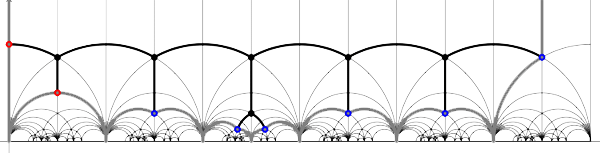
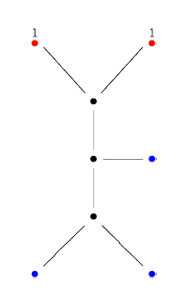
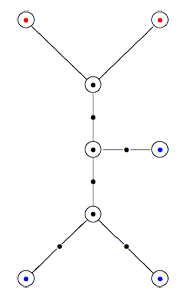For example, for the M(12) special polygon on the left (bounded by the thick black geodesics), the only vertices in $\mathbb{R} \cup \{ \infty \} $ are $\infty,0,\frac{1}{3},\frac{1}{2},1 $. The two vertical lines are free sides and are paired, whereas all other sides of the polygon are odd. Therefore the Farey-code for this Mathieu polygon is

[tex]\xymatrix{\infty \ar@{-}[r]_{1} & 0 \ar@{-}[r]_{\bullet} & \frac{1}{3} \ar@{-}[r]_{\bullet} & \frac{1}{2} \ar@{-}[r]_{\bullet} & 1 \ar@{-}[r]_{1} & \infty}[/tex]

Conversely, to a Farey-code we can associate a special polygon by first taking the hyperbolic convex hull of all the terms in the sequence (the region bounded by the vertical lines and the bottom red circles in the picture on the left) and adding to it for each odd interval [tex]\xymatrix{x_i \ar@{-}[r]_{\bullet} & x_{i+1}}[/tex] the triangle just outside the convex hull consisting of two odd edges in the Dedekind tessellation (then we obtain the region bounded by the black geodesics). Again, the side-pairing of the obained special polygon can be obtained from that of the Farey-code.

This correspondence gives a natural one-to-one correspondence special polygons <---> Farey-codes . _Later_ we will see how the Farey-code determines the group structure of the corresponding finite index subgroup of the modular group $\Gamma = PSL_2(\mathbb{Z}) $.

Reference

Ravi S. Kulkarni, “An arithmetic-geometric method in the study of the subgroups of the modular group”, Amer. J. Math 113 (1991) 1053-1133

Hyperbolic Mathieu polygons

Published June 27, 2007 by lieven

Today we will link modular quilts (via their associated cuboid tree diagrams) to special hyperbolic polygons. The above drawing gives the hyperbolic polygon (the gray boundary) associated to the M(24) tree diagram (the black interior graph). In general, the correspondence goes as follows.

Recall that a cuboid tree diagram is a tree such that all internal vertices are 3-valent and have a specified ordering on the incident edges (given by walking counterclockwise around the vertex) and such that all leaf-vertices are tinted blue or red, the latter ones are paired via an involution (indicated by giving paired red vertices the same label). Introduce a new 2-valent vertex on all edges joining two internal vertices or a blue vertex to an internal vertex. So, the picture on the right corresponds to the tree diagram on the left. Equip this extended tree with a metric such that every edge has length equal to an f-edge in the Dedekind tessellation. Fix an edge having a red vertex and develop this isometrically onto the f-edge connecting $i $ to $\rho $ in the tessellation. Then, the extended tree develops uniquely along the f-edges of the tessellation and such that the circled black and blue vertices correspond to odd vertices, the circled red and added uncircled vertices correspond to even vertices in the tessellation. Starting from the above tree (and choosing the upper-left edge to start the embedding), we obtain the picture on the left (we have removed the added 2-valent vertices)

We will now associate a special hyperbolic polygon to this tree. At a red vertex take the even line going through the vertex. If under the involution the red vertex is send to itself, the even edges will be paired. Otherwise, the line is a free side and will be paired to the free side containing the red vertex corresponding under the involution. At a blue vertex, take the two odd edges making an angle of $\frac{\pi}{3} $ with the tree-edge containing the blue vertex. These odd edges will be paired. If we do this procedure for all blue and red vertices, we obtain a special polygon (see the picture on the right, the two vertical lines are paired).
Conversely, suppose we start with a special polygon such as the one on the left below

and consider all even and odd vertices on the boundary (which are tinted red, respectively blue) together with all odd vertices in the interior of the special polygon. These are indicated in the picture on the right above. If we connect these vertices with the geodesics in the polygon we get a cuboid tree diagram. This correspondence special polygons —>> tree diagrams is finite to one as we have made a choice in the starting red vertex and edge. If we would have taken the other edge containing a red vertex we would end up with the following special polygon

It is no accident that these two special polygons consist of exactly 24 triangles of the Dedekind tessellation as they correspond to the index 12 subgroup of the modular group $\Gamma $ determining the 12-dimensional permutation representation of the Mathieu group $M_{12} $. Similarly, the top drawing has 48 hyperbolic triangles and corresponds to the 24-dimensional permutation representation of $M_{24} $. Another time we will make the connection with Farey series which will allow us to give free generators of finite index subgroups.

Reference

Ravi S. Kulkarni, “An arithmetic-geometric method in the study of the subgroups of the modular group”, Amer. J. Math. 113 (1991) 1053-1133

Category: featured

Hexagonal Moonshine (2)

Farey codes

Hyperbolic Mathieu polygons