Mathieu’s blackjack is a two-person combinatorial game played with 12 cards of values 0,1,2,…,11. For example take from any deck the numbered cards together with the jack (value 11) and the queen (value 0) (btw. if you find this PI by all means replace the queen by a zero-valued king). Shuffle the cards and divide them into two piles of 6 cards (all of them face up on the table) : the main-pile and the other-pile. The rules of the game are
- players alternate moves
- a move consists of exchanging a card of the main-pile with a lower-valued card from the other-pile
- the player whose move makes the sum of all cards in the main-pile under 21 looses the game
For example, the starting main-pile might consist of the six cards






This pile has total value 3+4+7+8+9+11=42. A move replaces one of these cards with a lowever vlued one not in the pile. So for example, replacing 8 with 5 or 1 or 2 or the queen are all valid moves. A winning move from this situation is for example replacing 8 by the queen (value 0) decreasing the value from 42 to 34






But there are otthers, such as replacing 11 by 5, 9 by 1 or 4 by 2. To win this game you need to know the secrets of the tetracode and the MINIMOG.
The tetracode is a one-error correcting code consisting of the following nine words of length four over $\mathbb{F}_3 = { 0,+,- } $
$~\begin{matrix} 0~0 0 0 & 0~+ + + & 0~- – – \\ +~0 + – & +~+ – 0 & +~- 0 + \\ -~0 – + & -~+ 0 – & -~- + 0 \end{matrix} $
The first element (which is slightly offset from the rest) is the slope s of the words, and the other three digits cyclically increase by s (in the field $\mathbb{F}_3 $). Because the Hamming-distance is 3 (the minimal number of different digits between two codewords), the tetracode can correct one error, meaning that if at most one of the four digits gets distorted by the channel one can detect and correct this. For example, if you would receive the word $+~++- $ (which is not a codeword) and if you would know that at most one digits went wrong, you can deduce that the word $+~0+- $ was sent. Thus, one can solve the 4-problem for the tetracode : correctt a tetracodeword given all 4 of its digits, one of which may be mistaken.
Another easy puzzle is the 2-problem for the tertracode : complete a tetracodeword from any 2 of its digits. For example, given the incomplete word $?~?0+ $ you can decide that the slope should be + and hence that the complete word must be $+~-0+ $.
We will use the MINIMOG here as a way to record the blackjack-position. It is a $4 \times 3 $ array where the 12 boxes correspond to the card-values by the following scheme
$\begin{array}{|c|ccc|} \hline 6 & 3 & 0 & 9 \\ 5 & 2 & 7 & 10 \\ 4 & 1 & 8 & 11 \\ \hline \end{array} $
and given a blackjack-position we place a star in the corresponding box, so the above start-position (resp. after the first move) corresponds to
$~\begin{array}{|c|ccc|} \hline & \ast & & \ast \\ & & \ast & \\ \ast & & \ast & \ast \\ \hline – & 0 & 0 & + \end{array}~ $ respectively $\begin{array}{|c|ccc|} \hline & \ast & \ast & \ast \\ & & \ast & \\ \ast & & & \ast \\ \hline – & 0 & – & + \end{array} $
In the final row we have added elements of $\mathbb{F}_3 $ indicating wher ethe stars are placed in that column (if there is just one star, we write the row-number of the star (ordered 0,+,- from top to bottom), if there are two stars we record the row-number of the empty spot. If we would have three or no stars in a column we would record a wild-card character : ?
 Observe that the final row of the start position is $-~00+ $ which is NOT a tetracodeword, whereas that of the winning position $-~0-+ $ IS a tetracodeword! This is the essence of the _Conway-Ryba winning strategy_ for Mathieu’s blackjack. There are precisely 132 winning positions forming the Steiner-system S(5,6,12). By an S(5,6,12) we mean a collection of 6-element subsets (our card-piles) from a 12-element set (the deck minus the king) having the amazing property that for EVERY 5-tuple from the 12-set there is a UNIQUE 6-element set containing this 5-tuple. Hence, there are exactly $\begin{pmatrix} 12 \\\ 5 \end{pmatrix}/6 = 132 $ elements in a Steiner S(5,6,12) system. The winning positions are exactly those MINOMOGs having 6 stars such that the final row is a tetracodeword (or can be extended to a tetracodeword replacing the wildcards ? by suitable digits) and such that the distribution of the stars over the columns is NOT (3,2,1,0) in any order.
Observe that the final row of the start position is $-~00+ $ which is NOT a tetracodeword, whereas that of the winning position $-~0-+ $ IS a tetracodeword! This is the essence of the _Conway-Ryba winning strategy_ for Mathieu’s blackjack. There are precisely 132 winning positions forming the Steiner-system S(5,6,12). By an S(5,6,12) we mean a collection of 6-element subsets (our card-piles) from a 12-element set (the deck minus the king) having the amazing property that for EVERY 5-tuple from the 12-set there is a UNIQUE 6-element set containing this 5-tuple. Hence, there are exactly $\begin{pmatrix} 12 \\\ 5 \end{pmatrix}/6 = 132 $ elements in a Steiner S(5,6,12) system. The winning positions are exactly those MINOMOGs having 6 stars such that the final row is a tetracodeword (or can be extended to a tetracodeword replacing the wildcards ? by suitable digits) and such that the distribution of the stars over the columns is NOT (3,2,1,0) in any order.
Provided the given blackjack-position is not in this Steiner-system (and there is only a 1/7 chance that it is), the strategy is clear : remove one of the stars to get a 5-tuple and determine the unique 6-set of the Steiner-system containing this 5-tuple. If the required extra star corresponds to a value less than the removed star you have a legal and winning move (if not, repeat this for another star). Finding these winning positions means solving 2- and 4-problems for the tetracode. _Another time_ we will say more about this Steiner system and indicate the relation with the Mathieu group $M_{12} $.
References
J.H. Conway and N.J.A. Sloane, ‘The Golay codes and the Mathieu groups’, chp. 10 of “Sphere Packings, Lattices and Groups“
David Joyner and Ann Casey-Luers, ‘Kittens, S(5,6,12) and Mathematical blackjack in SAGE‘
Leave a Comment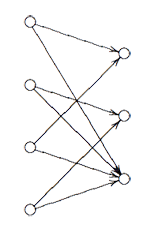 Here, the vertex spaces on the left are the iso-typical factors of $V \downarrow_{D_2} $ and those on the right those of $V \downarrow_{D_3} $ and the arrows give the block-components of the $C_2 $-isomorphism $\phi $. The nice things is that one can also reverse this process to get all $\tilde{\Gamma} $-representations from $\theta $-semistable representations of this quiver (having the additional condition that the square matrix made of the arrows is invertible) and isomorphisms of group-representation correspond to those of quiver-representations!
Here, the vertex spaces on the left are the iso-typical factors of $V \downarrow_{D_2} $ and those on the right those of $V \downarrow_{D_3} $ and the arrows give the block-components of the $C_2 $-isomorphism $\phi $. The nice things is that one can also reverse this process to get all $\tilde{\Gamma} $-representations from $\theta $-semistable representations of this quiver (having the additional condition that the square matrix made of the arrows is invertible) and isomorphisms of group-representation correspond to those of quiver-representations!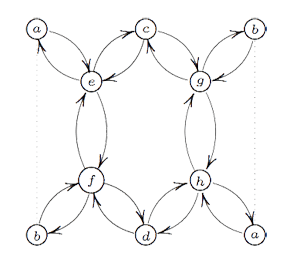 If one calculates the ‘clan’ of these 8 simples one obtains the double quiver of the graph on the left. Note that a and b appear twice, so one should glue the left and right hand sides together as a Moebius-strip. That is, the clan determining the representation theory of the extended modular group is a Moebius strip made of two hexagons!
If one calculates the ‘clan’ of these 8 simples one obtains the double quiver of the graph on the left. Note that a and b appear twice, so one should glue the left and right hand sides together as a Moebius-strip. That is, the clan determining the representation theory of the extended modular group is a Moebius strip made of two hexagons!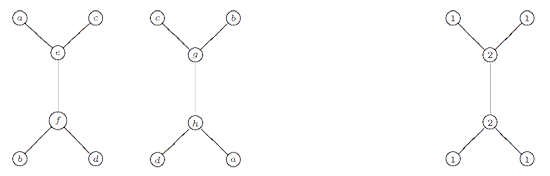
 By a result of
By a result of  Kulkarni’s result states that these matrices are free generators of the cofiniite modular subgroup determined by the Farey code. For example, for the
Kulkarni’s result states that these matrices are free generators of the cofiniite modular subgroup determined by the Farey code. For example, for the