Skip to content →

Category: featured

the iguanodon dissected

Published November 9, 2007 by lieven

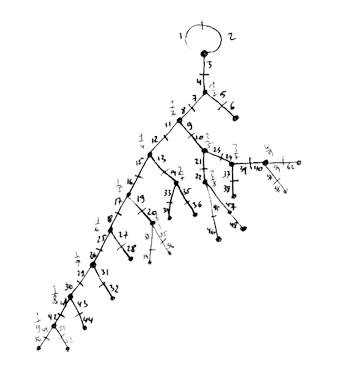
Here the details of the iguanodon series. Start with the Farey sequence $F(n) $of order n which is the sequence of completely reduced fractions between 0 and 1 which, when in lowest terms, have denominators less than or equal to n, arranged in order of increasing size. Here are the first eight Fareys

F(1) = {0โ„1, 1โ„1}
F(2) = {0โ„1, 1โ„2, 1โ„1}
F(3) = {0โ„1, 1โ„3, 1โ„2, 2โ„3, 1โ„1}
F(4) = {0โ„1, 1โ„4, 1โ„3, 1โ„2, 2โ„3, 3โ„4, 1โ„1}
F(5) = {0โ„1, 1โ„5, 1โ„4, 1โ„3, 2โ„5, 1โ„2, 3โ„5, 2โ„3, 3โ„4, 4โ„5, 1โ„1}
F(6) = {0โ„1, 1โ„6, 1โ„5, 1โ„4, 1โ„3, 2โ„5, 1โ„2, 3โ„5, 2โ„3, 3โ„4, 4โ„5, 5โ„6, 1โ„1}
F(7) = {0โ„1, 1โ„7, 1โ„6, 1โ„5, 1โ„4, 2โ„7, 1โ„3, 2โ„5, 3โ„7, 1โ„2, 4โ„7, 3โ„5, 2โ„3, 5โ„7, 3โ„4, 4โ„5, 5โ„6, 6โ„7, 1โ„1}
F(8) = {0โ„1, 1โ„8, 1โ„7, 1โ„6, 1โ„5, 1โ„4, 2โ„7, 1โ„3, 3โ„8, 2โ„5, 3โ„7, 1โ„2, 4โ„7, 3โ„5, 5โ„8, 2โ„3, 5โ„7, 3โ„4, 4โ„5, 5โ„6, 6โ„7, 7โ„8, 1โ„1}

Farey sequences have plenty of mysterious properties. For example, in 1924 J. Franel and Edmund Landau proved that an asymptotic density result about Farey sequences is equivalent to the Riemann hypothesis.
More precisely, let a(n) be the number of terms in the Farey sequence F(n) (that is, a(1)=2,a(2)=3,…,a(8)=23 etc. This is sequence A005728 in the online integer sequences catalog).
Let $F(n)_j $ denote the j-th term in F(n), then the following conjecture is equivalent to the Riemann hypothesis

For every $\epsilon > 0 $ there is a constant C depending on $\epsilon $ such that

$\sum_{j=1}^{a(n)} | F(n)_j – \frac{j}{a(n)} | < C n^{\frac{1}{2}+\epsilon} $

when n goes to infinity. Anyway, let us continue our construction. Farey sequences are clearly symmetric around 1/2 so let us just take half of them, so we jump to 1 when we have reached 1/2. Let us extend this halved Farey on both sides with $\infty $ and call it the modified Farey sequence f(n). For example,

$f(3) = {~\infty,0,\frac{1}{3},\frac{1}{2},1,\infty } $

Now consider the Farey code in which we identify the two sides connected to $\infty $ and mark two consecutive Farey numbers as

[tex]\xymatrix{f(n)_i \ar@{-}[r]_{\bullet} & f(n)_{i+1}}[/tex]

That is, the Farey code associated to the modified sequence f(3) is

[tex]\xymatrix{\infty \ar@{-}[r]_{1} & 0 \ar@{-}[r]_{\bullet} & \frac{1}{3} \ar@{-}[r]_{\bullet} & \frac{1}{2} \ar@{-}[r]_{\bullet} & 1 \ar@{-}[r]_{1} & \infty}[/tex]

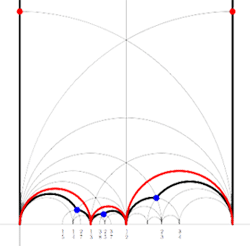Recall from earlier that to a Farey-code we can associate a special polygon by first taking the hyperbolic convex hull of all the terms in the sequence (the region bounded by the vertical lines and the bottom red circles in the picture on the left) and adding to it for each odd interval [tex]\xymatrix{f(n)_i \ar@{-}[r]_{\bullet} & f(n)_{i+1}}[/tex] the triangle just outside the convex hull consisting of two odd edges in the Dedekind tessellation (then we obtain the region bounded by the black geodesics for the sequence f(3)).

Next, we can associate to this special polygon a cuboid tree diagram by considering all even and odd vertices on the boundary (which are tinted red, respectively blue) together with all odd vertices in the interior of the special polygon. These are indicated in the left picture below. If we connect these vertices with the geodesics in the polygon we get a cuboid tree diagram. The obtained cuboid tree diagram is depicted on the right below.

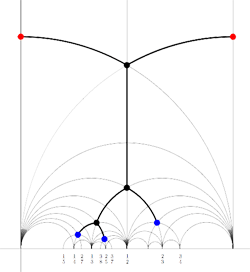
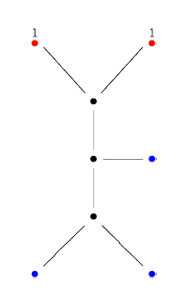
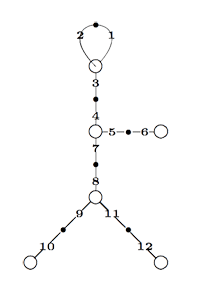Finally, identifying the red points (as they lie on geodesics connected to $\infty $ which are identified in the Farey code), adding even points on the remaining geodesics and numbering the obtained half-lines we obtain the dessin d’enfant given on the left hand side. To such a dessin we can associate its monodromy group which is a permutation group on the half-lines generated by an order two element indicating which half-lines make up a line and an order three element indicating which half-lines one encounters by walking counter-clockwise around a three-valent vertex. For the dessin on the left the group is therefore the subgroup of $S_{12} $ generated by the elements

$\alpha = (1,2)(3,4)(5,6)(7,8)(9,10)(11,12) $

$\beta = (1,2,3)(4,5,7)(8,9,11) $

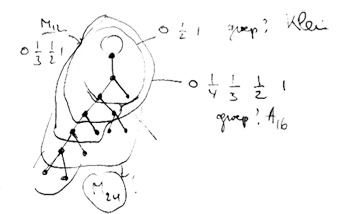
and a verification with GAP tells us that this group is the sporadic Mathieu group $M_{12} $. This concludes the description of the second member of the Iguanodon series. If you like to check that the first 8 iguanodons are indeed the simple groups

$L_2(7), M_{12}, A_{16}, M_{24}, A_{28}, A_{40}, A_{48}, A_{60}, \ldots $

the following dissection of the Iguanodon may prove useful

Leave a Comment

Iguanodon series of simple groups

Published November 7, 2007 by lieven

Bruce Westbury has a page on recent work on series of Lie groups including exceptional groups. Moreover, he did put his slides of a recent talk (probably at MPI) online.

Probably, someone considered a similar problem for simple groups. Are there natural constructions leading to a series of finite simple groups including some sporadic groups as special members ? In particular, does the following sequence appear somewhere ?

$L_2(7), M_{12}, A_{16}, M_{24}, A_{28}, A_{40}, A_{48}, A_{60}, \ldots $

Here, $L_2(7) $ is the simple group of order 168 (the automorphism group of the Klein quartic), $M_{12} $ and $M_{24} $ are the sporadic Mathieu groups and the $A_n $ are the alternating simple groups.

I’ve stumbled upon this series playing around with Farey sequences and their associated ‘dessins d’enfants’ (I’ll come back to the details of the construction another time) and have dubbed this sequence the Iguanodon series because the shape of the doodle leading to its first few terms

reminded me of the Iguanodons of Bernissart (btw. this sketch outlines the construction to the experts). Conjecturally, all groups appearing in this sequence are simple and probably all of them (except for the first few) will be alternating.

I did verify that none of the known low-dimensional permutation representations of other sporadic groups appear in the series. However, there are plenty of similar sequences one can construct from the Farey sequences, and it would be nice if one of them would contain the Conway group $Co_1 $. (to be continued)

Leave a Comment

M-geometry (3)

Published September 18, 2007 by lieven

For any finite dimensional A-representation S we defined before a character $\chi(S) $ which is an linear functional on the noncommutative functions $\mathfrak{g}_A = A/[A,A]_{vect} $ and defined via

$\chi_a(S) = Tr(a | S) $ for all $a \in A $

We would like to have enough such characters to separate simples, that is we would like to have an embedding

$\mathbf{simp}~A \hookrightarrow \mathfrak{g}_A^* $

from the set of all finite dimensional simple A-representations $\mathbf{simp}~A $ into the linear dual of $\mathfrak{g}_A^* $. This is a consequence of the celebrated Artin-Procesi theorem.

Michael Artin was the first person to approach representation theory via algebraic geometry and geometric invariant theory. In his 1969 classical paper “On Azumaya algebras and finite dimensional representations of rings” he introduced the affine scheme $\mathbf{rep}_n~A $ of all n-dimensional representations of A on which the group $GL_n $ acts via basechange, the orbits of which are exactly the isomorphism classes of representations. He went on to use the Hilbert criterium in invariant theory to prove that the closed orbits for this action are exactly the isomorphism classes of semi-simple -dimensional representations. Invariant theory tells us that there are enough invariant polynomials to separate closed orbits, so we would be done if the caracters would generate the ring of invariant polynmials, a statement first conjectured in this paper.

Claudio Procesi was able to prove this conjecture in his 1976 paper “The invariant theory of $n \times n $ matrices” in which he reformulated the fundamental theorems on $GL_n $-invariants to show that the ring of invariant polynomials of m $n \times n $ matrices under simultaneous conjugation is generated by traces of words in the matrices (and even managed to limit the number of letters in the words required to $n^2+1 $). Using the properties of the Reynolds operator in invariant theory it then follows that the same applies to the $GL_n $-action on the representation schemes $\mathbf{rep}_n~A $.

So, let us reformulate their result a bit. Assume the affine $\mathbb{C} $-algebra A is generated by the elements $a_1,\ldots,a_m $ then we define a necklace to be an equivalence class of words in the $a_i $, where two words are equivalent iff they are the same upto cyclic permutation of letters. For example $a_1a_2^2a_1a_3 $ and $a_2a_1a_3a_1a_2 $ determine the same necklace. Remark that traces of different words corresponding to the same necklace have the same value and that the noncommutative functions $\mathfrak{g}_A $ are spanned by necklaces.

The Artin-Procesi theorem then asserts that if S and T are non-isomorphic simple A-representations, then $\chi(S) \not= \chi(T) $ as elements of $\mathfrak{g}_A^* $ and even that they differ on a necklace in the generators of A of length at most $n^2+1 $. Phrased differently, the array of characters of simples evaluated at necklaces is a substitute for the clasical character-table in finite group theory.

Leave a Comment