214066877211724763979841536000000000000

If you Googled this number a week ago, all you’d get were links to the paper by Melanie Wood Belyi-extending maps and the Galois action on dessins d’enfants.

In this paper she says she can separate two dessins d’enfants (which couldn’t be separated by other Galois invariants) via the order of the monodromy group of the inflated dessins by a certain degree six Belyi-extender.

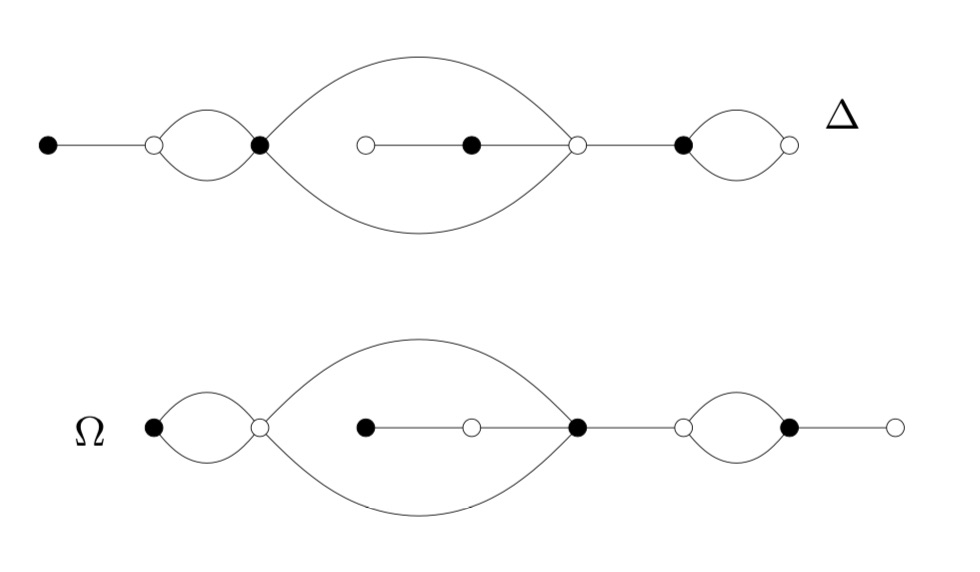
She gets for the inflated $\mathrm{\Delta }$ the order 19752284160000 and for inflated $\mathrm{\Omega }$ the order 214066877211724763979841536000000000000 (see also this post).

After that post I redid the computations a number of times (as well as for other Belyi-extenders) and always find that these orders are the same for both dessins.

And, surprisingly, each time the same numbers keep popping up.

For example, if you take the Belyi-extender $t^6$ (power-map) then it is pretty easy to work out the generators of the monodromy group of the extended dessin.

For example, there is a cycle $(1,2)$ in $x_{\mathrm{\Omega }}$ and you have to replace it by
$$(11,12,13,14,15,16,21,22,23,24,25,26)$$
and similarly for other cycles, always replace number $k$ by $k1,k2,k3,k4,k5,k6$ (these are the labels of the edges in the extended dessin corresponding to edge $k$ in the original dessin, starting to count from the the ‘spoke’ of the $6$-star of $t^6$ corresponding to the interval $(0,e^{\frac{4\pi i}{3}})$, going counterclockwise). So the edge $(0,1)$ corresponds to $k3$, and for $y$ you take the same cycles as in $y_{\mathrm{\Omega }}$ replacing number $k$ by $k3$.

Here again, you get for both extended diagrams the same order of the monodromy group, and surprise, surprise: it is 214066877211724763979841536000000000000.

Based on these limited calculations, it seems to be that the order of the monodromy group of the extended dessin only depends on the degree of the extender, and not on its precise form.

I’d hazard a (probably far too optimistic) conjecture that the order of the monodromy groups of a dessin $\mathrm{\Gamma }$ and the extended dessin $\gamma (\mathrm{\Gamma })$ for a Belyi-extender $\gamma$ of degree $d$ are related via
$$\mathrm{\#}M(\gamma (\mathrm{\Gamma }))=d\times (\mathrm{\#}M(\mathrm{\Gamma }){)}^d$$
(or twice that number), except for trivial settings such as power-maps extending stars.

Edit (august 19): In the comments Dominic shows that in “most” cases the monodromy group of $\gamma (\mathrm{\Gamma })$ should be the wreath product on the monodromy groups of $\gamma$ and $\mathrm{\Gamma }$ which has order
$$\mathrm{\#}M(\mathrm{\Gamma }{)}^d\times \mathrm{\#}M(\gamma )$$
which fits in with the few calculations i did.

We knew already that the order of the monodromy groups op $\mathrm{\Delta }$ and $\mathrm{\Omega }$ is $1814400$, and sure enough
$$6\times {1814400}^6=214066877211724763979841536000000000000.$$

If you extend $\mathrm{\Delta }$ and $\mathrm{\Omega }$ by the power map $t^3$, you get the orders
$$17919272189952000000=3\times {1814400}^3$$
and if you extend them with the degree 3 extender mentioned in the dessinflateurs-post you get 35838544379904000000, which is twice that number. (Edit : the order of the monodromy group of the extender is $6$, see also above)

As much as i like the Belyi-extender idea to construct new Galois invariants, i fear it’s a dead end. (Always glad to be proven wrong!)